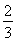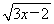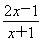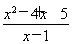题目内容
已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值为8,求二次函数f(x)的解析式.
f(x)=-4x2+4x+7
【解析】(解法1:利用一般式)设f(x)=ax2+bx+c(a≠0), 解得
解得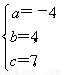
∴所求二次函数为f(x)=-4x2+4x+7.
(解法2:利用顶点式)设f(x)=a(x-m)2+n,∵f(2)=f(-1),∴抛物线对称轴为x=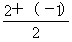 =
= ,即m=
,即m=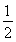 ;又根据题意,函数最大值ymax=8,
;又根据题意,函数最大值ymax=8,
∴n=8,∴f(x)=a 2+8.∵f(2)=-1,∴a
2+8.∵f(2)=-1,∴a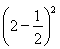 +8=-1,解得a=-4.
+8=-1,解得a=-4.
∴f(x)=-4 2+8=-4x2+4x+7.
2+8=-4x2+4x+7.
(解法3:利用两根式)由题意知f(x)+1=0的两根为x1=2,x2=-1,故可设f(x)+1=a(x-2)(x+1),即f(x)=ax2-ax-2a-1.又函数有最大值ymax=8,即 =8,解得a=-4或a=0(舍),∴所求函数的解析式为f(x)=-4x2-(-4)x-2×(-4)-1=-4x2+4x+7
=8,解得a=-4或a=0(舍),∴所求函数的解析式为f(x)=-4x2-(-4)x-2×(-4)-1=-4x2+4x+7

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目