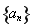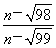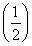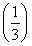题目内容
已知函数f(x)=x2+mx+n的图象过点(1,3),且f(-1+x)=f(-1-x)对任意实数都成立,函数y=g(x)与y=f(x)的图象关于原点对称.
(1)求f(x)与g(x)的解析式;
(2)若F(x)=g(x)-λf(x)在(-1,1]上是增函数,求实数λ的取值范围.
(1)g(x)=-x2+2x(2)(-∞,0].
【解析】(1)因为函数f(x)满足f(-1+x)=f(-1-x)对任意实数都成立,
所以图象关于x=-1对称,即-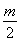 =-1,即m=2.
=-1,即m=2.
又f(1)=1+m+n=3,所以n=0,所以f(x)=x2+2x.
又y=g(x)与y=f(x)的图象关于原点对称,
所以-g(x)=(-x)2+2(-x),
所以g(x)=-x2+2x.
(2)由(1)知,F(x)=(-x2+2x)-λ(x2+2x)=-(λ+1)x2+(2-2λ)x.
当λ+1≠0时,F(x)的对称轴为x=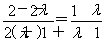 ,
,
因为F(x)在(-1,1]上是增函数,
所以 或
或
所以λ<-1或-1<λ≤0.
当λ+1=0,即λ=-1时,F(x)=4x显然成立.
综上所述,实数λ的取值范围是(-∞,0].

练习册系列答案
相关题目