题目内容
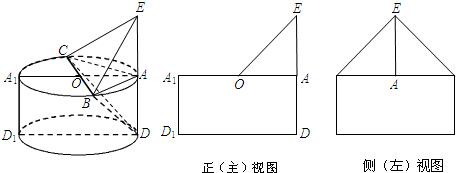
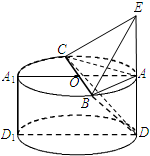
一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A、B、C在圆O的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图2所示,其中EA⊥平面ABC,AB⊥AC,AB=AC,AE=2.
(1)求证:AC⊥BD;
(2)求三棱锥E-BCD的体积.

(1)求证:AC⊥BD;
(2)求三棱锥E-BCD的体积.
(1)证明:因为EA⊥平面ABC,AC?平面ABC,所以EA⊥AC,即ED⊥AC.
又因为AC⊥AB,AB∩ED=A,所以AC⊥平面EBD.
因为BD?平面EBD,所以AC⊥BD.(4分)
(2)因为点A、B、C在圆O的圆周上,且AB⊥AC,所以BC为圆O的直径.
设圆O的半径为r,圆柱高为h,根据正(主)视图、侧(左)视图的面积可得,
(6分)
解得
所以BC=4,AB=AC=2
.
以下给出求三棱锥E-BCD体积的两种方法:
方法1:由(1)知,AC⊥平面EBD,
所以VE-BCD=VC-EBD=
S△EBD×CA.(10分)
因为EA⊥平面ABC,AB?平面ABC,
所以EA⊥AB,即ED⊥AB.
其中ED=EA+DA=2+2=4,因为AB⊥AC,AB=AC=2
,
所以S△EBD=
×ED×AB=
×4×2
=4
.(13分)
所以VE-BCD=
×4
×2
=
.(14分)
方法2:因为EA⊥平面ABC,
所以VE-BCD=VE-ABC+VD-ABC=
S△ABC×EA+
S△ABC×DA=
S△ABC×ED.(10分)
其中ED=EA+DA=2+2=4,因为AB⊥AC,AB=AC=2
,
所以S△ABC=
×AC×AB=
×2
×2
=4.(13分)
所以VE-BCD=
×4×4=
.(14分)
又因为AC⊥AB,AB∩ED=A,所以AC⊥平面EBD.
因为BD?平面EBD,所以AC⊥BD.(4分)
(2)因为点A、B、C在圆O的圆周上,且AB⊥AC,所以BC为圆O的直径.
设圆O的半径为r,圆柱高为h,根据正(主)视图、侧(左)视图的面积可得,
|
解得
|
所以BC=4,AB=AC=2
| 2 |
以下给出求三棱锥E-BCD体积的两种方法:
方法1:由(1)知,AC⊥平面EBD,
所以VE-BCD=VC-EBD=
| 1 |
| 3 |
因为EA⊥平面ABC,AB?平面ABC,
所以EA⊥AB,即ED⊥AB.
其中ED=EA+DA=2+2=4,因为AB⊥AC,AB=AC=2
| 2 |
所以S△EBD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
所以VE-BCD=
| 1 |
| 3 |
| 2 |
| 2 |
| 16 |
| 3 |
方法2:因为EA⊥平面ABC,
所以VE-BCD=VE-ABC+VD-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
其中ED=EA+DA=2+2=4,因为AB⊥AC,AB=AC=2
| 2 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
所以VE-BCD=
| 1 |
| 3 |
| 16 |
| 3 |


练习册系列答案
相关题目