题目内容
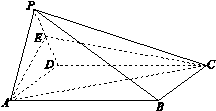
如图,三棱锥P-ABC中,PA=a,AB=AC=2a,∠PAB=∠PAC=∠BAC=60°,求三棱锥P-ABC的体积.
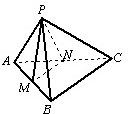

如图,取AB、AC的中点M、N,连接PM,PN,MN,
则PA=AM=AN=a,由∠PAB=∠PAC=∠BAC=60°,
得:PM=PN=MN=a,∴三棱锥P-AMN是棱长为a的正四面体,它的体积为,
VP-AMN=
•S△AMN•h=
×
×a2×sin60°×
=
a3;
三棱锥P-ABC的体积为,VP-ABC=
•S△ABC•h=
×4•S△AMN•h=4VP-AMN=
a3.

则PA=AM=AN=a,由∠PAB=∠PAC=∠BAC=60°,
得:PM=PN=MN=a,∴三棱锥P-AMN是棱长为a的正四面体,它的体积为,
VP-AMN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
a2-(
|
| ||
| 12 |
三棱锥P-ABC的体积为,VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |


练习册系列答案
相关题目
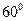 的菱形,则该棱柱的体积等于( )
的菱形,则该棱柱的体积等于( )