题目内容
【题目】已知椭圆![]() ,四点
,四点![]() ,
,![]() ,
,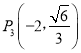 ,
,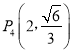 中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
中恰有三个点在椭圆C上,左、右焦点分别为F1、F2.
(1)求椭圆C的方程;
(2)过左焦点F1且不平行坐标轴的直线l交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线x=﹣3于点M,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆的对称性可得P2,P3,P4在椭圆上,进而求出椭圆的方程;
(2)由(1)可得F1的坐标,由题意设直线l的方程与椭圆联立,求出两根之和及两根之积,求出PQ的中点N的坐标,再由直线ON与x=﹣3,求出M的坐标,进而求出![]() 的表达式,换元由二次函数配方可得其最大值.
的表达式,换元由二次函数配方可得其最大值.
解:(1)由椭圆的对称性易知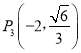 ,
, 关于y轴对称,
关于y轴对称,
一定都在椭圆上.所以![]() 一定不在椭圆上.
一定不在椭圆上.
根据题意![]() 也在椭圆上,
也在椭圆上,
将![]() ,
, 带入椭圆方程,解得椭圆方程为
带入椭圆方程,解得椭圆方程为![]() ;
;
(2)设直线l方程为y=k(x+2)(k≠0),P(x1,y1),Q(x2,y2),
联立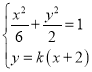 ,可得(3k2+1)x2+12k2x+12k2﹣6=0;
,可得(3k2+1)x2+12k2x+12k2﹣6=0;
则![]() =24(k2+1)>0,且
=24(k2+1)>0,且![]() ,
,![]() ,
,
设PQ的中点N(x0,y0),则![]() ,
,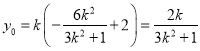 ,
,
∴N坐标为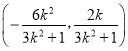 ,
,![]() ,;
,;
因此直线ON的方程为![]() ,从而点M为
,从而点M为![]() ,又F1(﹣2,0),
,又F1(﹣2,0),
所以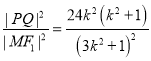 ,令u=3k2+1≥1,
,令u=3k2+1≥1,
则![]() ,
,
因此当u=4,即k=±1时h(u)最大值为3.
所以![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
【题目】新冠疫情发生后,酒精使用量大增,某生产企业调整设备,全力生产![]() 与
与![]() 两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量
两种不同浓度的酒精,按照计划可知在一个月内,酒精日产量![]() (单位:吨)与时间n(
(单位:吨)与时间n(![]() 且
且![]() )成等差数列,且
)成等差数列,且![]() ,
,![]() .又知
.又知![]() 酒精日产量所占比重
酒精日产量所占比重![]() 与时间n成等比数列,
与时间n成等比数列,![]() 酒精日产量所占比重与时间n的关系如下表(
酒精日产量所占比重与时间n的关系如下表(![]() ):
):
|
|
|
| …… |
时间n | 1 | 2 | 3 | …… |
(1)求![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,求前n天
,求前n天![]() (单位:吨,
(单位:吨,![]() 且
且![]() ).
).