��Ŀ����
����Ŀ���¹����鷢���ƾ�ʹ����������ij������ҵ�����豸��ȫ������![]() ��
��![]() ���ֲ�ͬŨ�ȵľƾ������ռƻ���֪��һ�����ڣ��ƾ��ղ���
���ֲ�ͬŨ�ȵľƾ������ռƻ���֪��һ�����ڣ��ƾ��ղ���![]() (��λ����)��ʱ��n(
(��λ����)��ʱ��n(![]() ��
��![]() )�ɵȲ����У���
)�ɵȲ����У���![]() ��
��![]() .��֪
.��֪![]() �ƾ��ղ�����ռ����
�ƾ��ղ�����ռ����![]() ��ʱ��n�ɵȱ����У�
��ʱ��n�ɵȱ����У�![]() �ƾ��ղ�����ռ������ʱ��n�Ĺ�ϵ���±�(
�ƾ��ղ�����ռ������ʱ��n�Ĺ�ϵ���±�(![]() )��
)��
|
|
|
| ���� |
ʱ��n | 1 | 2 | 3 | ���� |
��1����![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ����ǰn��
����ǰn��![]() (��λ���֣�
(��λ���֣�![]() ��
��![]() ).
).
���𰸡���1��![]() ��
��![]() (
(![]() )����2��
)����2��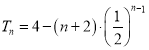 ��(
��(![]() ��
��![]() ).
).
��������
��1���ɵȲ�ȱ����еĶ����ͨ�ʽ����ã�
��2�����ô�λ������ɵô�.
��1����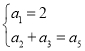 ����
����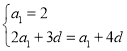 ������
������![]() ������
������![]() .
.
��Ϊ![]() ��
��![]() .����
.����![]() (
(![]() ).
).
��2��������֪����n��![]() �ƾ���������Ϊ
�ƾ���������Ϊ ��
��
![]()
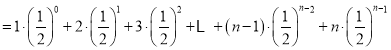 �٣�
�٣�
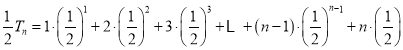 �ڣ�
�ڣ�
�ɢ�![]() �ڵã�
�ڵã�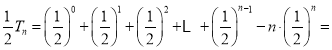
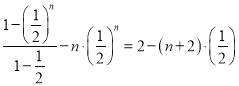 ��
��
����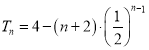 ��
��
���ϣ�ǰn��![]() �ƾ�����������
�ƾ�����������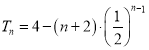 ��(
��(![]() ��
��![]() ).
).

����Ŀ����ij��˾200������������루��λ����Ԫ��ͳ�����±���1����ʾ��
���������� |
|
|
|
|
|
|
Ƶ�� | 12 | 28 | 36 | 54 | 50 | 20 |
Ƶ�� |
����1��
��1���������Ƶ�ʷֲ����������ƹ�˾��200����վ��������루ͬһ���е������ø�������������е�ֵ��������
��2����֪�ù�˾2020���һ�������ȵ��������������±���2����ʾ���������ȵ����������뼰��Ƶ�ʿ��ñ���1���е����ݽ��ƴ��棬����2020�꣬����˾����������Ϊ![]() ʱ��Ա�����ռ�ЧΪ100Ԫ������˾����������Ϊ
ʱ��Ա�����ռ�ЧΪ100Ԫ������˾����������Ϊ![]() ʱ��Ա�����ռ�ЧΪ200Ԫ������˾����������Ϊ
ʱ��Ա�����ռ�ЧΪ200Ԫ������˾����������Ϊ![]() ʱ��Ա�����ռ�ЧΪ300Ԫ.��Ƶ�ʹ��Ƹ���.
ʱ��Ա�����ռ�ЧΪ300Ԫ.��Ƶ�ʹ��Ƹ���.
�����ڵ�������ijԱ���Ĺ������������ȡ2�죬�Ǹ�Ա��2��ļ�Ч֮��Ϊ![]() ����
����![]() �ķֲ����Լ���ѧ������
�ķֲ����Լ���ѧ������
����ÿ��Ա��ÿ�����ȵĹ�����Ϊ50�죬����2020��ǰ��������ÿ��Ա����õļ�Ч���ܶ�.
���������� |
|
|
|
|
|
|
Ƶ�� | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
����2��