题目内容
【题目】某公司采购了一批零件，为了检测这批零件是否合格，从中随机抽测120个零件的长度（单位：分米），按数据分成
，
，
，
，
，
这6组，得到如图所示的频率分布直方图，其中长度大于或等于1.59分米的零件有20个，其长度分别为1.59，1.59，1.61，1.61，1.62，1.63，1.63，1.64，1.65，1.65，1.65，1.65，1.66，1.67，1.68，1.69，1.69，1.71，1.72，1.74，以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
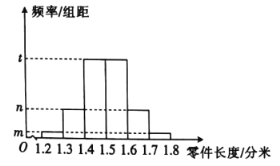
（1）求这批零件的长度大于1.60分米的频率，并求频率分布直方图中
，
，
的值；
（2）若从这批零件中随机选取3个，记
为抽取的零件长度在
的个数，求的分布列和数学期望；
（3）若变量
满足
且
，则称变量满足近似于正态分布
的概率分布.如果这批零件的长度
（单位：分米）满足近似于正态分布
的概率分布，则认为这批零件是合格的将顺利被签收；否则，公司将拒绝签收.试问，该批零件能否被签收？
【答案】（1）
，
，
；（2）分布列见解析，2.1；（3）能被该公司签收.
【解析】
（1）根据120件样本零件中长度大于1.60分米的共有18件即可求出频率，根据所给数据分别求出
，
两组的频率可得m,n，再根据频率之和为1求出t即可；
（2）由题意从这批零件中随机选取1件，长度在
的概率
，且服从二项分布，即可求解；、
（3）根据题意，验证零件数据对于
且
是否成立即可求解.
（1）由题意可知120件样本零件中长度大于1.60分米的共有18件，
则这批零件的长度大于1.60分米的频率为
，
记
为零件的长度，则
，
，
，
故
，
，
.
（2）由（1）可知从这批零件中随机选取1件，长度在的概率
.
且随机变量
服从二项分布
，
则
，
，
，
故随机变量的分布列为
| 0 | 1 | 2 | 3 |
| 0.027 | 0.189 | 0.441 | 0.343 |
（或
）.
（3）由题意可知
，
，
则
；
，
因为
，
，
所以这批零件的长度满足近似于正态分布
的概率分布.
应认为这批零件是合格的，将顺利被该公司签收.
