题目内容
【题目】自新冠肺炎疫情发生以来，某社区积极防范，并利用网络对本社区居民进行新冠肺炎防御知识讲座，为了解该社区居民对防御知识的掌握情况，随机调查了该社区100人，统计得到如下
列联表：
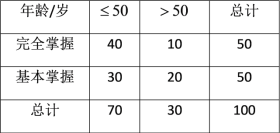
（1）请根据2x2列联表，判断是否有95%的把握认为防御知识掌握情况与年龄有关；
（2）为了进一步提高该社区的防御意识，该社区采用分层抽样的方法，从调查的完全掌握的居民中抽取10人，再从这10人中随机选取2人作为下一次讲座的讲解员，设X为这2人中年龄小于或等于50岁的人数，求
的分布列与数学期望.
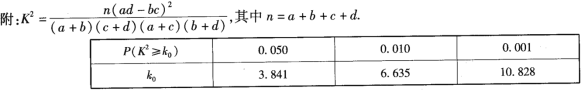
【答案】（1）有95%的把握认为防御知识掌握情况与年龄有关；（2）分布列见解析，
.
【解析】
（1）计算
，得到答案.
（2）根据分层抽样的比例关系得到人数，
的可能取值为
，计算概率得到分布列，计算数学期望得到答案.
（1）根据题意：
，
故有95%的把握认为防御知识掌握情况与年龄有关.
（2）根据分层抽样：
年龄小于等于50岁的有
人，年龄大于50岁的有
人，
则的可能取值为，
则
，
，
，
故分布列为：
|
|
|
|
|
|
|
|
故数学期望为
.
【题目】将某公司200天的日销售收入（单位：万元）统计如下表（1）所示，
日销售收入 |
|
|
|
|
|
|
频数 | 12 | 28 | 36 | 54 | 50 | 20 |
频率 |
表（1）
（1）完成上述频率分布表，并估计公司这200天的日均销售收入（同一组中的数据用该组所在区间的中点值代表）；
（2）已知该公司2020年第一、二季度的日销售收入如下表（2）所示，第三季度的日销售收入及其频率可用表（1）中的数据近似代替，且在2020年，当公司日销售收入为
时，员工的日绩效为100元，当公司日销售收入为
时，员工的日绩效为200元，当公司日销售收入为
时，员工的日绩效为300元.以频率估计概率.
①若在第三季度某员工的工作日中随机抽取2天，记该员工2天的绩效之和为
，求的分布列以及数学期望；
②若每个员工每个季度的工作日为50天，估计2020年前三个季度每个员工获得的绩效的总额.
日销售收入 |
|
|
|
|
|
|
频率 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
表（2）
