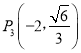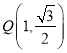题目内容
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
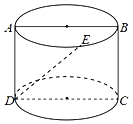
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
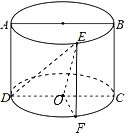
设CD的中点为O,过E作EF⊥底面⊙O,连接OE,OF,证明OD⊥OE,计算tan∠EDO即可得出答案.
∵AB//CD,∴∠EDC(或补角)为异面直线DE与AB所成的角,
设CD的中点为O,过E作EF⊥底面⊙O,连接OE,OF,
∵E是![]() 的中点,∴F是
的中点,∴F是![]() 的中点,∴CD⊥OF,
的中点,∴CD⊥OF,
又EF⊥平面⊙O,∴EF⊥CD,![]()
∴CD⊥平面OEF,∴OD⊥OE.
设AD=1,则CD![]() ,故OF
,故OF![]() ,EF=1,
,EF=1,
于是OE![]() ,
,
∴tan∠EDO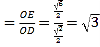 ,
,
∴∠EDO![]() .
.
故选:C.

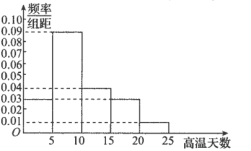
【题目】将某公司200天的日销售收入(单位:万元)统计如下表(1)所示,
日销售收入 |
|
|
|
|
|
|
频数 | 12 | 28 | 36 | 54 | 50 | 20 |
频率 |
表(1)
(1)完成上述频率分布表,并估计公司这200天的日均销售收入(同一组中的数据用该组所在区间的中点值代表);
(2)已知该公司2020年第一、二季度的日销售收入如下表(2)所示,第三季度的日销售收入及其频率可用表(1)中的数据近似代替,且在2020年,当公司日销售收入为![]() 时,员工的日绩效为100元,当公司日销售收入为
时,员工的日绩效为100元,当公司日销售收入为![]() 时,员工的日绩效为200元,当公司日销售收入为
时,员工的日绩效为200元,当公司日销售收入为![]() 时,员工的日绩效为300元.以频率估计概率.
时,员工的日绩效为300元.以频率估计概率.
①若在第三季度某员工的工作日中随机抽取2天,记该员工2天的绩效之和为![]() ,求
,求![]() 的分布列以及数学期望;
的分布列以及数学期望;
②若每个员工每个季度的工作日为50天,估计2020年前三个季度每个员工获得的绩效的总额.
日销售收入 |
|
|
|
|
|
|
频率 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 | 0.1 |
表(2)