题目内容
(本小题满分16分)
已知圆M的圆心M在y轴上,半径为1.直线 被圆M所截得的弦长为
被圆M所截得的弦长为 ,且圆心M在直线
,且圆心M在直线 的下方.
的下方.
(1)求圆M的方程;
(2)设 若AC,BC是圆M的切线,求
若AC,BC是圆M的切线,求 面积的最小值.
面积的最小值.
已知圆M的圆心M在y轴上,半径为1.直线
 被圆M所截得的弦长为
被圆M所截得的弦长为 ,且圆心M在直线
,且圆心M在直线 的下方.
的下方.(1)求圆M的方程;
(2)设
 若AC,BC是圆M的切线,求
若AC,BC是圆M的切线,求 面积的最小值.
面积的最小值.(1)圆M的方程为
(2) 的面积的最小值为
的面积的最小值为 .
.

(2)
 的面积的最小值为
的面积的最小值为 .
.解:(1)设 由题设知,M到直线
由题设知,M到直线 的距离是
的距离是 …………2分
…………2分
所以 解得
解得 ………………4分
………………4分
因为圆心M在直线 的下方,所以
的下方,所以 ,
,
即所求圆M的方程为 ………………6分
………………6分
(2)当直线AC,BC 的斜率都存在,即
的斜率都存在,即 时
时
直线AC的斜率
同理直线BC的斜率 ……………
…………… …8分
…8分
所以直线AC的方程为
直线BC的方程为 ………………10分
………………10分
解方程组 得……
得…… ……12分
……12分
所以
因为 所
所 以
以 所以
所以 .
.
故当 时,
时, 的面
的面 积取最小值
积取最小值 .………………14分
.………………14分
当直线AC,BC的斜率有一个不存在时,即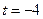 或
或 时,易求得
时,易求得 的面积为
的面积为 .
.
综上,当 时,
时, 的面积的最小值为
的面积的最小值为 .………………16分
.………………16分
 由题设知,M到直线
由题设知,M到直线 的距离是
的距离是 …………2分
…………2分所以
 解得
解得 ………………4分
………………4分因为圆心M在直线
 的下方,所以
的下方,所以 ,
,即所求圆M的方程为
 ………………6分
………………6分(2)当直线AC,BC
 的斜率都存在,即
的斜率都存在,即 时
时直线AC的斜率

同理直线BC的斜率
 ……………
…………… …8分
…8分所以直线AC的方程为

直线BC的方程为
 ………………10分
………………10分解方程组
 得……
得…… ……12分
……12分所以

因为
 所
所 以
以 所以
所以 .
.故当
 时,
时, 的面
的面 积取最小值
积取最小值 .………………14分
.………………14分当直线AC,BC的斜率有一个不存在时,即
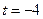 或
或 时,易求得
时,易求得 的面积为
的面积为 .
.综上,当
 时,
时, 的面积的最小值为
的面积的最小值为 .………………16分
.………………16分
练习册系列答案
相关题目
 本小题满分12分)
本小题满分12分)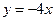 上,且与直线
上,且与直线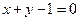 相切于
相切于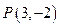
 的圆的方程.
的圆的方程.
 已知关于x,y的方程C:
已知关于x,y的方程C: .
. ,求m的值。
,求m的值。 中,以
中,以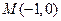 为圆心的圆与直线
为圆心的圆与直线 相切.
相切. 的方程;
的方程; 对称,求
对称,求 的值.
的值. 、
、 ,圆内的动点
,圆内的动点 满足
满足 ,求
,求 的取值范围.
的取值范围.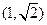 的直线
的直线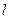 将圆
将圆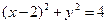 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线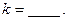
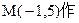 圆
圆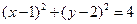 的切线,则切线方程为 ( )
的切线,则切线方程为 ( )



 上任一点
上任一点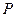 向圆
向圆 作两条切线,切点为
作两条切线,切点为 .则
.则 最大值为
最大值为 
 ( )
( )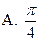



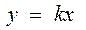 被圆
被圆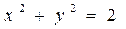 所截得的弦AB的长等于
所截得的弦AB的长等于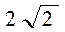
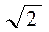
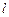 :
: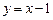 被该圆所截得的弦长为
被该圆所截得的弦长为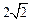 ,则圆C的标准方程为 .
,则圆C的标准方程为 .