题目内容
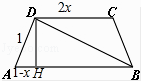
【题目】在等腰梯形ABCD中，AB∥CD，且|AB|=2，|AD|=1，|CD|=2x其中x∈（0，1），以A，B为焦点且过点D的双曲线的离心率为e1 ， 以C，D为焦点且过点A的椭圆的离心率为e2 ， 若对任意x∈（0，1）不等式t＜e1+e2恒成立，则t的最大值为（ ）
A.
B.
C.2
D.
【答案】B
【解析】解：在等腰梯形ABCD中，BD2=AD2+AB2﹣2ADABcos∠DAB
=1+4﹣2×1×2×（1﹣x）=1+4x，
由双曲线的定义可得a1= 
，c1=1，e1= 
，
由椭圆的定义可得a2= 
，c2=x，e2= 
，
则e1+e2= + = + ，
令t= 
∈（0， 
﹣1），
则e1+e2= 
（t+ 
）在（0， ﹣1）上单调递减，
所以e1+e2＞ ×（ ﹣1+ 
）= ，
故选：B．
练习册系列答案
相关题目
