题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]()
(1)求椭圆![]() 的标准方程
的标准方程
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆与不同的两点
交椭圆与不同的两点![]() ,且满足
,且满足![]() (其中
(其中![]() 为坐标原点)。若存在,求出直线
为坐标原点)。若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【答案】(1)![]() ;(2)存在直线
;(2)存在直线![]() 或
或![]() 满足题意.
满足题意.
【解析】
(1)根据已知得到关于a,b,c的方程组,解方程组即得解.(2)对直线l的斜率分类讨论,直线![]() 的斜率必存在,不妨设为
的斜率必存在,不妨设为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,联立直线和椭圆的方程得到
,联立直线和椭圆的方程得到![]() ,得到
,得到![]() ,把韦达定理代入向量的数量积,得到k的值.即得直线的方程.
,把韦达定理代入向量的数量积,得到k的值.即得直线的方程.
(1)∵椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]()
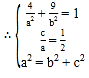 ,解得
,解得![]() ,
,
∴椭圆的方程为![]()
(2)假设存在过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,且满足
,且满足![]()
若直线![]() 的斜率不存在,且直线过点
的斜率不存在,且直线过点![]() ,则直线
,则直线![]() 即为
即为![]() 轴所在直线
轴所在直线
∴直线![]() 与椭圆的两不同交点
与椭圆的两不同交点![]() 就是椭圆短轴的端点,
就是椭圆短轴的端点,
![]()
![]()
∴直线![]() 的斜率必存在,不妨设为
的斜率必存在,不妨设为![]() ,
,
∴可设直线![]() 的方程为
的方程为![]() ,即
,即![]()
联立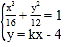 ,消
,消![]() 得
得![]() ,
,
∵直线与椭圆相交于不同的两点![]() ,
,
![]() 得:
得: ![]() 或
或![]() ①
①
设![]() ,
,
![]()
![]()
又![]() ,
,
![]()
化简得![]() ,
,
![]() 或
或![]() ,经检验均满足①式,
,经检验均满足①式,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() ,
,
∴存在直线![]() 或
或![]() 满足题意.
满足题意.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
【题目】已知某产品的广告费用x(单位:万元)与销售额y(单位:万元)具有线性关系关系,其统计数据如下表:
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,据此模型预报广告费用为8万元时的销售额是( )
,据此模型预报广告费用为8万元时的销售额是( )
附: ![]() =
= 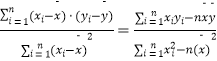 ;
; ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
A.59.5
B.52.5
C.56
D.63.5
