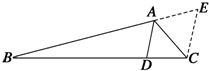
题目内容
19.无穷等差数列{an}的各项均为整数,首项为a1,公差为d,Sn是其前n项和,3,21,15是其中的三项,给出下列命题,真命题有( )①对任意满足条件的d,存在a1,使得99一定是数列{an}中的一项.
②对任意满足条件的d,存在a1,使得30一定是数列{an}中的一项.
③存在满足条件的数列{an},使得对任意的n∈N*,S2n=4Sn成立.
| A. | ①③ | B. | ①② | C. | ②③ | D. | ①②③ |
分析 利用等差数列的公式,分别讨论前n项和3、21、15的具体项数,然后进行推理即可.首先根据条件得出d≤6;①99-21=78能被6整除,且=13,假设15和21之间有n项,那么99和21之间有13n项,得出结论;②30-21=9不能被6整除,如果d=6,那么30一定不是数列{an}中的一项,得出结论.③利用等差数列的前n项和公式化简S2n=4Sn,得出结论.
解答 解:要使等差数列的公差最大,则3,15,21因为相邻的前n项和,此时对应两项为15-3=12,21-15=6,所以d≤6.
①99-21=78能被6整除,且$\frac{78}{6}$=13,假设15和21之间有n项,那么99和21之间有13n项,所以99一定是数列{an}中的一项,所以①正确.
②30-21=9不能被6整除,如果d=6,那么30一定不是数列{an}中的一项,所以②错误.
③如果有S2n=4Sn,那么由等差数列求和公式有:2na1+n(2n-1)•d=4[na1+$\frac{n(n-1)}{2}$d],化简得到,d=2a1,所以只要满足条件d=2a1的数列{an},就能使得对任意的n∈N*,S2n=4Sn成立,所以③正确.
故选:A.
点评 本题考查等差数列的通项公式及前n项和公式的应用,解题的关键是根据条件得出公差.考查学生分析问题,解决问题的能力,综合性较强,难度较大.

练习册系列答案
相关题目
9.一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分,则这串珠子被盒子遮住的部分有( )颗.
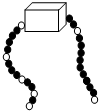

| A. | 3 | B. | 5 | C. | 10 | D. | 27 |
7.如图,由若干圆点组成如三角形的图形,每条边(包括两个端点)有n(n>1,n∈N)个点,每个图形总的点数记为an,则$\frac{9}{{{a_2}{a_3}}}+\frac{9}{{{a_3}{a_4}}}+\frac{9}{{{a_4}{a_5}}}+…+\frac{9}{{{a_{2014}}{a_{2015}}}}$=( )


| A. | $\frac{2014}{2015}$ | B. | $\frac{2013}{2014}$ | C. | $\frac{3}{2015}$ | D. | $\frac{9}{2015}$ |
14.设全集U=Z,集合M={1,2},P={-2,-1,0,1,2},则P∩CUM=( )
| A. | {0} | B. | {1} | C. | {-1,-2,0} | D. | Φ |
4.已知集合A={x∈R|-4<x<1,},集合B={x∈R|(x+3)(x-2)<0},且A∩B=( )
| A. | {x|-4<x<1} | B. | {x|-4<x<-3} | C. | {x|-3<x<1} | D. | {x|-3<x<2} |
11.下列结论正确的是( )
| A. | 当$x∈(0,\frac{π}{2})$时,$sinx+\frac{1}{sinx}≥2$ | B. | 当x>0时,$\sqrt{x}+\frac{1}{{\sqrt{x}}}≥2$ | ||
| C. | 当x≥2时,$x+\frac{1}{x}$的最小值为2 | D. | 当0<x≤2时,$x-\frac{1}{x}$无最大值 |
8.现有6个人分乘两辆不同的出租车,已知每辆车最多能乘坐4个人,则不同的乘车方案种数为( )
| A. | 30 | B. | 50 | C. | 60 | D. | 70 |
9.已知正四棱柱(底面为正方形,侧棱垂直于底面的四棱柱)ABCD-A1B1C1D1中,AA1=$\sqrt{2}$AB,E为AA1中点,则异面直线BE与C1D所成角的余弦为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | 0 |