题目内容
【题目】已知![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若关于![]() 的不等式
的不等式![]() 能成立,求实数
能成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() .
.
【解析】
(1)运用绝对值的意义,去绝对值,解不等式,求并集即可;
(2)求得|t﹣1|+|2t+3|的最小值![]() ,原不等式等价为
,原不等式等价为![]() |x+l|﹣|x﹣m|的最大值,由绝对值不等式的性质,以及绝对值不等式的解法,可得所求范围.
|x+l|﹣|x﹣m|的最大值,由绝对值不等式的性质,以及绝对值不等式的解法,可得所求范围.
解:(1)由题意可得|x﹣1|+|2x+3|>4,
当x≥1时,x﹣1+2x+3>4,解得x≥1;
当![]() x<1时,1﹣x+2x+3>4,解得0<x<1;
x<1时,1﹣x+2x+3>4,解得0<x<1;
当x![]() 时,1﹣x﹣2x﹣3>4,解得x<﹣2.
时,1﹣x﹣2x﹣3>4,解得x<﹣2.
可得原不等式的解集为(﹣∞,﹣2)∪(0,+∞);
(2)由(1)可得|t﹣1|+|2t+3|
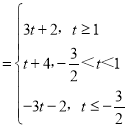 ,
,
可得t![]() 时,|t﹣1|+|2t+3|取得最小值
时,|t﹣1|+|2t+3|取得最小值![]() ,
,
关于x的不等式|x+l|﹣|x﹣m|≥|t﹣1|+|2t+3|(t∈R)能成立,
等价为![]() |x+l|﹣|x﹣m|的最大值,
|x+l|﹣|x﹣m|的最大值,
由|x+l|﹣|x﹣m|≤|m+1|,可得|m+1|![]() ,
,
解得m![]() 或m
或m![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
