题目内容
18.用计算机随机产生的有序二元数组(x,y)满足-1<x<1,-1<y<1.(1)求事件x≤$\frac{1}{2}$的概率;
(2)求事件“x2+y2>1”的概率.
分析 (1)求出事件“x≤$\frac{1}{2}$”为事件A的测度为2,事件A的表示的区域d为数轴上-1到$\frac{1}{2}$的线段,测度为$\frac{3}{2}$,然后求解P(A).
(2)记事件“x2+y2>1”事件为B,求出B测度为4,事件B表示的平面区域d'为圆O的外部,则其测度,然后求解事件“x2+y2>1”的概率.
解答 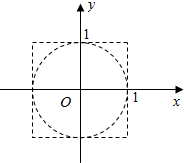 解:(1)记事件“x≤$\frac{1}{2}$”为事件A,…(1分)
解:(1)记事件“x≤$\frac{1}{2}$”为事件A,…(1分)
x可以看成数轴上的点,则所有试验结果形成的区域D为数轴上-1到1的线段,其测度为2,…(3分)
事件A的表示的区域d为数轴上-1到$\frac{1}{2}$的线段,测度为$\frac{3}{2}$,…(5分)
P(A)=$\frac{d的测度}{D的测度}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$.
答:事件x≤$\frac{1}{2}$的概率为$\frac{3}{4}$.…(7分)
(2)记事件“x2+y2>1”事件为B,…(8分)
由于x,y的随机性,(x,y)可以看成坐标平面中的点,
所有试验的全部结果D'为{(x,y)|-1<x<1,-1<y<1}表示的平面区域,是边长为2正方形,测度为4,…(10分)
事件B表示的平面区域d'为圆O的外部,则其测度为(4-π)…(12分)
则:$P(B)=\frac{d'的测度}{D'的测度}=\frac{4-π}{4}$,
答:事件“x2+y2>1”的概率为$\frac{4-π}{4}$.…(14分)
点评 本题考查几何概型的概率的求法,考查计算能力.

练习册系列答案
相关题目
9.设f(x)=cosx-sinx,把f(x)的图象按向量$\overrightarrow{a}$=(m,0)(m>0)平移后,图象恰好为函数y=-f′(x)的图象,则m的值可以为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | π | D. | $\frac{π}{2}$ |
10.若函数y=ax+b-1(a>0且a≠1)的图象不经过第四象限,则有( )
| A. | a>1且b≥0 | B. | a>1且b≥1 | C. | 0<a<1且b≤0 | D. | 0<a<1且b≤1 |
7.在复平面内复数$z=\frac{ai+1}{1-i}$对应的点在第一象限,则实数a的取值可以为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
