题目内容
9.设f(x)=cosx-sinx,把f(x)的图象按向量$\overrightarrow{a}$=(m,0)(m>0)平移后,图象恰好为函数y=-f′(x)的图象,则m的值可以为( )| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | π | D. | $\frac{π}{2}$ |
分析 先求函数的导数,利用三角函数的平移关系,利用辅助角公式进行化简即可得到结论.
解答 解:函数的导数f′(x)=-sinx-cosx,
则y=-f′(x)=sinx+cosx=$\sqrt{2}$cos(x-$\frac{π}{4}$),
f(x)的图象按向量$\overrightarrow{a}$=(m,0)(m>0)平移后,得到y=cos(x-m)-sin(x-m)=$\sqrt{2}$cos(x-m+$\frac{π}{4}$),
则当-m+$\frac{π}{4}$=-$\frac{π}{4}$时,即m=$\frac{π}{2}$时,满足条件.
故选:D.
点评 本题主要考查函数图象的变化关系,求函数的导数,结合辅助角公式进行化简是解决本题的关键.

练习册系列答案
相关题目
4.三角形ABC中,A、B、C所对的边分别为a,b,c;若A=$\frac{π}{3}$,则$a(cosC+\sqrt{3}sinC)$=( )
| A. | a+b | B. | a+c | C. | b+c | D. | a+b+c |
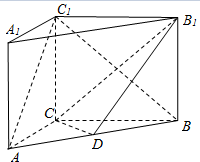 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.