题目内容
若等比数列{an}满足a2+a4=20,a3+a5=40,则数列{an}的前n项和Sn=________.
2n+1-2
设等比数列{an}的公比为q.
∵a2+a4=20,a3+a5=40.
∴a3+a5=(a2+a4)q=40,且a1q+a1q3=20,解之得q=2,且a1=2.
故Sn= =2n+1-2.
=2n+1-2.
∵a2+a4=20,a3+a5=40.
∴a3+a5=(a2+a4)q=40,且a1q+a1q3=20,解之得q=2,且a1=2.
故Sn=
 =2n+1-2.
=2n+1-2.
练习册系列答案
相关题目
 ,
, ,…,
,…, ,…是首项为1,公比为-
,…是首项为1,公比为- 的等比数列,则a5等于________.
的等比数列,则a5等于________. +
+ ≥2
≥2
 =4a1,则
=4a1,则 的最小值为( ).
的最小值为( ).






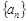 中,若
中,若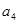 ,
,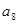 是方程
是方程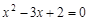 的两根,则
的两根,则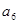 的值是( )
的值是( )


