题目内容
16.设f-1(x)为f(x)=$\frac{x}{2x+1}$的反函数,则f-1(2)=-$\frac{2}{3}$.分析 由原函数解析式把x用含有y的代数式表示,x,y互换求出原函数的反函数,则f-1(2)可求.
解答 解:由y=f(x)=$\frac{x}{2x+1}$,得$x=\frac{y}{1-2y}$,
x,y互换可得,$y=\frac{x}{1-2x}$,即f-1(x)=$\frac{x}{1-2x}$.
∴${f}^{-1}(2)=\frac{2}{1-2×2}=-\frac{2}{3}$.
故答案为:$-\frac{2}{3}$.
点评 本题考查了函数的反函数的求法,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设z1、z2∈C,则“z1、z2均为实数”是“z1-z2是实数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
8.设z1,z2∈C,则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
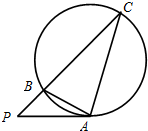 如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.
如图,过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,PB=3,AB=4,则AC=8.