题目内容
方程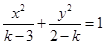 表示焦点在
表示焦点在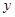 轴的双曲线,则
轴的双曲线,则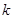 的取值范围是( )
的取值范围是( )
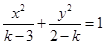 表示焦点在
表示焦点在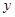 轴的双曲线,则
轴的双曲线,则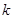 的取值范围是( )
的取值范围是( )A.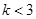 | B.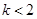 | C.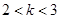 | D.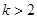 |
B
试题分析:方程
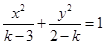 变形为
变形为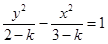 ,因为表示焦点在y轴上的双曲线,所以满足
,因为表示焦点在y轴上的双曲线,所以满足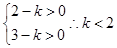
点评:双曲线焦点位置的确定是看
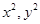 的系数哪一个系数为正,焦点就在哪一个坐标轴上
的系数哪一个系数为正,焦点就在哪一个坐标轴上
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
题目内容
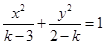 表示焦点在
表示焦点在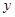 轴的双曲线,则
轴的双曲线,则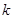 的取值范围是( )
的取值范围是( )A.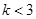 | B.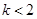 | C.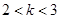 | D.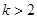 |
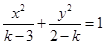 变形为
变形为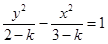 ,因为表示焦点在y轴上的双曲线,所以满足
,因为表示焦点在y轴上的双曲线,所以满足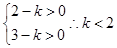
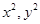 的系数哪一个系数为正,焦点就在哪一个坐标轴上
的系数哪一个系数为正,焦点就在哪一个坐标轴上
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案