题目内容
9.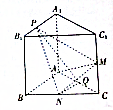 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.(1)证明:无论点P怎样运动,总有AM⊥平面PNQ;
(2)是否存在点P,使得平面PMN与平面PNQ所成的锐二面角为45°?若存在,试确定点P的位置;若不存在,请说明理由.
分析 (1)建立空间直角坐标系,设出棱长,得到点的坐标,由向量数量积证得答案;
(2)求出平面PMN的法向量、平面PNQ的法向量,利用向量的夹角公式,结合平面PMN与平面PNQ所成的锐二面角为45°,即可得出结论.
解答 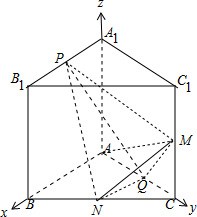 (1)证明:建立如图所示的空间直角坐标系,设AA1=AB=AC=a,
(1)证明:建立如图所示的空间直角坐标系,设AA1=AB=AC=a,
则A(0,0,0),M(0,a,$\frac{a}{2}$),N($\frac{a}{2}$,$\frac{a}{2}$,0),Q(0,$\frac{a}{2}$,0),
A1(0,0,a),B1(a,0,a),
再设P(x,0,a),由A1P=λA1B1,得$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$(λ>0),
即(x,0,0)=λ(a,0,0),即x=λa,
∴P(λa,0,a),
∵$\overrightarrow{PN}$=($\frac{a}{2}$-λa,$\frac{a}{2}$,-a),$\overrightarrow{PQ}$=(-λa,$\frac{a}{2}$,-a),$\overrightarrow{AM}$=(0,a,$\frac{a}{2}$),
∴$\overrightarrow{AM}•\overrightarrow{PN}$=0,$\overrightarrow{AM}•\overrightarrow{PQ}$=0,则AM⊥平面PNQ;
(Ⅱ)解:设平面PMN的法向量为$\overrightarrow{n}$=(x,y,z),则
∵$\overrightarrow{PN}$=($\frac{a}{2}$-λa,$\frac{a}{2}$,-a),$\overrightarrow{MN}$=($\frac{a}{2}$,-$\frac{a}{2}$,-$\frac{a}{2}$),
∴$\left\{\begin{array}{l}{(\frac{a}{2}-λa)x+\frac{ay}{2}-az=0}\\{\frac{ax}{2}-\frac{ay}{2}-\frac{az}{2}=0}\end{array}\right.$,∴$\overrightarrow{n}$=(3,1+2λ,2-2λ)
同理平面PNQ的法向量为$\overrightarrow{m}$=(0,2,1),
∵平面PMN与平面PNQ所成的锐二面角为45°,
∴$\frac{2(1+2λ)+(2-2λ)}{\sqrt{9+(1+2λ)^{2}+(2-2λ)^{2}}}$•$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,∴λ=-$\frac{1}{2}$,与λ>0矛盾.
∴不存在点P,使得平面PMN与平面PNQ所成的锐二面角为45°.
点评 利用向量知识解决立体几何问题的优点在于用代数化的方法解决立体几何,解题的关键在于用坐标表示空间向量,是中档题.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
| A. | ② | B. | ①② | C. | ①③ | D. | ①②③ |
| A. | 2k+2 | B. | 2k+3 | C. | 2k+1 | D. | (2k+2)+(2k+3) |
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{30}}{6}$ | D. | $\frac{\sqrt{30}}{10}$ |