题目内容
19.在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,AA1=2,则异面直线A1B与B1C所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{30}}{6}$ | D. | $\frac{\sqrt{30}}{10}$ |
分析 如图所示,建立空间直角坐标系.利用向量的夹角公式即可得出.
解答 解:如图所示,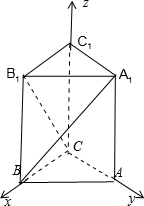
建立空间直角坐标系.
C(0,0,0),B(1,0,0),A1(0,1,2),
B1(1,0,2),
$\overrightarrow{{A}_{1}B}$=(1,-1,-2),$\overrightarrow{C{B}_{1}}$=(1,0,2).
∴$cos<\overrightarrow{{A}_{1}B},\overrightarrow{C{B}_{1}}>$=$\frac{\overrightarrow{{A}_{1}B}•\overrightarrow{C{B}_{1}}}{|\overrightarrow{{A}_{1}B}||\overrightarrow{C{B}_{1}}|}$=$\frac{1-4}{\sqrt{6}×\sqrt{5}}$=-$\frac{\sqrt{30}}{10}$.
∴异面直线A1B与B1C所成角的余弦值为$\frac{\sqrt{30}}{10}$.
故选:D.
点评 本题考查了利用向量的夹角公式求异面直线所成的夹角,考查了计算能力,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
7.已知f是有序数对集合M={(x,y)|x∈N*,y∈N*}上的一个映射,正整数数对(x,y)在映射f下对应的为实数z,记作f(x,y)=z.对于任意的正整数m,n(m>n),映射f由下表给出:
则使不等式f(2,x)≤3的解集为{1,2}.
| (x,y) | (n,n) | (m,n) | (n,m) |
| f(x,y) | n | m-n | m+n |
4.已知△ABC中的内角为A,B,C,重心为G,若2sinA$\overrightarrow{GA}$+$\sqrt{3}$sinB$\overrightarrow{GB}$+3sinC$\overrightarrow{GC}$=$\overrightarrow{0}$,则cosB=( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
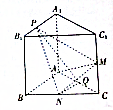 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.