题目内容
1.用数学归纳法证明1+2+3+…+(2n+1)=(n+1)(2n+1)时,从n=k到n=k+1,左边需增添的代数式是( )| A. | 2k+2 | B. | 2k+3 | C. | 2k+1 | D. | (2k+2)+(2k+3) |
分析 从式子1+2+22+…+25n-1是观察当n=1时的值以及当从n=k到n=k+1的变化情况,从而解决问题.
解答 解:当n=1时,原式的值为1+2+22+23+24=31,1+2+3=(1+1)(2+1)
当n=k时,原式左侧:1+2+3+…+(2k+1),
∴从k到k+1时需增添的项是(2k+2)+(2k+3)
故选:D.
点评 本题主要考查数学归纳法,数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基)2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.

练习册系列答案
相关题目
6.已知定义域为R的函数f(x)满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(2,f((2))处的切线方程是( )
| A. | 4x-y+4=0 | B. | 4x-y-4=0 | C. | 4x+y+4=0 | D. | 4x+y-4=0 |
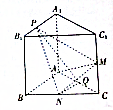 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动. 已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.
已知空间四边形OABC,如图所示,其对角线为OB,AC.M,N分别为OA,BC的中点,点G在线段MN上,且$\overrightarrow{MG}$=2$\overrightarrow{GN}$,现用基向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$表示向量$\overrightarrow{OG}$,并设$\overrightarrow{OG}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=$\frac{5}{6}$.