题目内容
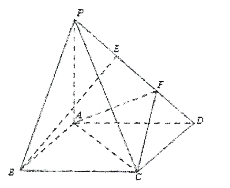
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
【答案】①③④
【解析】
在①中,由AB⊥平面CDE,知异面直线AB与CD所成角为90°;在②中,直线AB与平面BCD所成角为![]() ;在③中由EF∥AC,知直线EF∥平面ACD;在④中,由BC⊥平面ADF,知平面AFD⊥平面BCD,从而得到结果
;在③中由EF∥AC,知直线EF∥平面ACD;在④中,由BC⊥平面ADF,知平面AFD⊥平面BCD,从而得到结果
解:正四面体ABCD中,点E,F分别是AB,BC的中点,
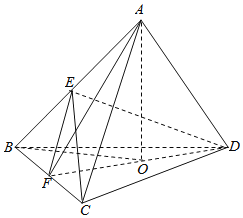
在①中,∵正四面体ABCD中,点E、F分别是AB,BC的中点,
∴CE⊥AB,DE⊥AB,
又![]() ,∴AB⊥平面CDE,
,∴AB⊥平面CDE,
∵CD平面CDE,
∴![]() ,即异面直线AB与CD所成角为90°,故①正确;
,即异面直线AB与CD所成角为90°,故①正确;
在②中,过A作AO⊥平面BCD,交DF=O,连结BO,
则∠ABO是直线AB与平面BCD所成角,
设正四面体ABCD的棱长为2,
则DF=![]() ,BO=
,BO=![]() ,
,
cos![]() =
=![]() =
=![]()
∴直线AB与平面BCD所成角为![]() ,故②错误;
,故②错误;
在③中,∵点E、F分别是AB,BC的中点,
∴EF∥AC,
∵EF![]() 平面ACD,AC平面ACD,
平面ACD,AC平面ACD,
∴直线EF∥平面ACD,故③正确;
在④中,由AF⊥BC,DF⊥BC,
又![]() ,∴BC⊥平面ADF,
,∴BC⊥平面ADF,
∵BC平面BCD,∴平面AFD⊥平面BCD,故④正确
故答案为:①③④

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目