Question

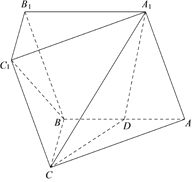
【题目】如图，在三棱柱中，侧面为菱形， 且是的中点．

(1)求证：∥平面；

(2)求证：平面平面.

Answer 1

【答案】（1）证明见解析；（2）证明见解析。

【解析】

（1）连结C1A，设AC1∩A1C=E，连结DE．由三角形中位线定理得到DE∥BC1．由此能证明BC1∥平面A1DC；

（2）由已知条件得△A1AB为正三角形，从而得到 ，AB⊥CD，进而得到AB⊥平面A1DC，由此能证明平面A1DC⊥平面ABC．

（1）证明：连结，设，连结．

∵三棱柱的侧面是平行四边形，∴为中点．

在△中，又∵是的中点，∴∥．

∵平面，平面，∴ ∥平面．

(2)∵ 为菱形，且， ∴△为正三角形．

是的中点，∴．

∵，是的中点，∴ ．

，∴平面．

∵平面，∴平面平面．