题目内容
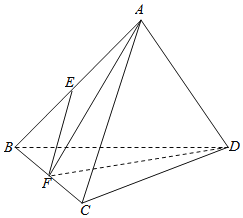
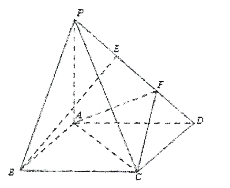
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() 为
为![]() 的两个三等分点.
的两个三等分点.
(1)求证![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)连结BD,AC相交于O,证明BE∥OF,即可证明BE∥平面ACF;(2)过A作AH⊥PC于H,利用面面垂直的性质证明AH⊥平面PCD,从而证明AH⊥CD,然后利用线面垂直的性质证明PC⊥CD.
(Ⅰ)连接BD、AC,两线交于O,
∴O是BD的中点(平行四边形对角线互相平分),
∵F是DE的中点(由三等分点得到),
∴OF是△DEB的中位线,∴BE∥OF,
∵OF面ACF,BE面ACF,
∴BE平行平面ACF.
(Ⅱ)过A作AH⊥PC于H,∵平面PAC⊥平面PCD,
∴AH⊥平面PCD,∵CD平面PCD,∴AH⊥CD,
∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.又∵PA∩AH=A,∴CD⊥平面PAC,
∵PC平面PAC,
∴PC⊥CD.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目