题目内容
19. 在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明:
在正三棱柱ABC-A1B1C1中,点D是AB的中点,证明:(1)BC1∥平面CDA1;
(2)平面ABB1A1⊥平面CDA1.
分析 (1)连接AC1交A1C于点G,连接DG,在正三棱柱ABC-A1B1C1中,四边形ACC1A1是平行四边形,则AG=GC1,而AD=DB,则DG∥BC1,DG?平面A1DC,BC1?平面A1DC,根据线面平行的判定定理可知BC1∥平面A1DC;
(2)由正三棱柱的结构特征可知平面ABB1A1⊥平面ABC,再由D为AB的中点,得CD⊥AB,则CD⊥平面ABB1A1,由平面与平面垂直的判定得答案.
解答 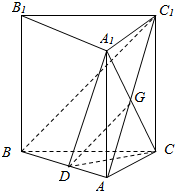 证明:(1)连接AC1交A1C于点G,连接DG,
证明:(1)连接AC1交A1C于点G,连接DG,
在正三棱柱ABC-A1B1C1中,四边形ACC1A1是平行四边形,
∴AG=GC1,
∵AD=DB,
∴DG∥BC1
∵DG?平面A1DC,BC1?平面A1DC,
∴BC1∥平面A1DC;
(2)∵ABC-A1B1C1是正三棱柱,
∴平面ABB1A1⊥平面ABC,
∵D为AB的中点,∴CD⊥AB,则CD⊥平面ABB1A1,
而CD?平面ABC,
∴平面ABB1A1⊥平面CDA1.
点评 本题考查直线与平面平行的判定,考查了平面与平面垂直的判断,考查学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
9.命题p:x>4;命题q:4<x<10,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}$+$\frac{π}{12}$ | B. | 1+$\frac{π}{12}$ | C. | $\frac{1}{3}$$+\frac{π}{4}$ | D. | 1$+\frac{π}{4}$ |
14.a、b为任意实数,若(a,b)在曲线f(x,y)=0上,且(b,a)也在曲线f(x,y)=0上,则曲线f(x,y)=0的几何特征是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
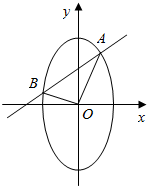 已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.
已知椭圆C的方程为x2+$\frac{{y}^{2}}{4}$=1,定点N(0,1),过圆M:x2+y2=$\frac{4}{5}$上任意一点作圆M的一条切线交椭圆C于A、B两点.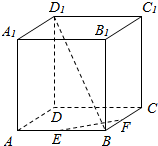 在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.
在正方体ABCD-A1B1C1D1中,E、F分别是AB,BC的中点,求异面直线BD1、EF所成角的大小.