题目内容
2.已知函数f(x)=x3+bx2+cx,对任意的b,c∈[-3,3].f(x)在(-1,1)内既有极大值又有极小值的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 求导数,确定f(x)在(-1,1)内既有极大值又有极小值,对应的区域的面积,b,c∈[-3,3],对应区域的面积,即可求出f(x)在(-1,1)内既有极大值又有极小值的概率.
解答 解:由题意f′(x)=3x2+2bx+c,
∵f(x)在(-1,1)内既有极大值又有极小值,
∴f′(x)=3x2+2bx+c=0的两个根在(-1,1)内,
∴$\left\{\begin{array}{l}{4{b}^{2}-12c>0}\\{-1<-\frac{b}{3}<1}\\{3-2b+c>0}\\{3+2b+c>0}\end{array}\right.$,对应区域的面积为2${∫}_{0}^{3}(\frac{1}{3}{b}^{2}-2b+3)$=$(\frac{1}{9}{b}^{3}-{b}^{2}+3b){|}_{0}^{3}$=6,
∵b,c∈[-3,3],
∴对应区域的面积为36,
∴f(x)在(-1,1)内既有极大值又有极小值的概率为$\frac{1}{6}$,
故选:D.
点评 本题考查函数的极值,考查导数知识的运用,考查概率的计算,确定区域,正确求面积是关键.

练习册系列答案
相关题目
17.某班的一次数学考试后,按学号统计前20名同学的考试成绩如茎叶图所示,则该样本数据的中位数为( )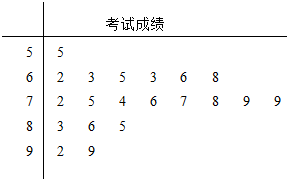

| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
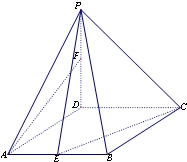 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.