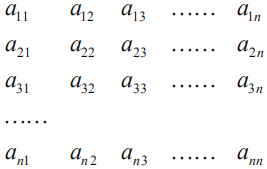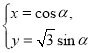题目内容
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
【答案】![]()
【解析】
根据题意可知函数f(x)是一个周期为2e的偶函数,即可作出函数f(x)在[﹣e,3e]上的图象,由方程的根与两函数图象交点的横坐标的关系可求得![]() 的值,再利用二倍角公式化简函数
的值,再利用二倍角公式化简函数![]() ,然后根据平移法则即可求得
,然后根据平移法则即可求得![]() ,从而求得
,从而求得![]() .
.
因为f(e+x)=f(e﹣x),所以f(x)关于x=e对称,又因为偶函数f(x),
所以f(x)的周期为2e.
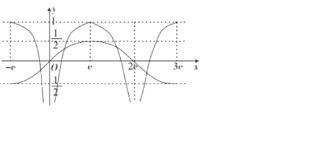
当x∈(0,e]时,f(x)=lnx,于是可作出函数f(x)在[﹣e,3e]上的图象如图所示,
方程![]() 的实数根是函数y=f(x)与函数
的实数根是函数y=f(x)与函数![]() 的交点的横坐标,
的交点的横坐标,
由图象的对称性可知,两个函数在[﹣e,3e]上有4个交点,且4个交点的横坐标之和为4e,所以4e=3ea,故a![]() ,
,
因为![]() ,
,
所以![]() ,
,
故![]() .
.
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?