题目内容
【题目】将n2个数排成n行n列的一个数阵，如图：该数阵第一列的n个数从上到下构成以m为公差的等差数列，每一行的n个数从左到右构成以m为公比的等比数列（其中m＞0）.已知a11＝2，a13＝a61+1，记这n2个数的和为S.下列结论正确的有（ ）
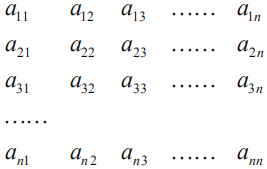
A.m＝3B.
C.
D.
【答案】ACD
【解析】
根据第一列成等差，第一行成等比可求出
，列式即可求出
，从而求出通项
，
再按照分组求和法，每一行求和可得S，由此可以判断各选项的真假．
∵a11＝2，a13＝a61+1，∴2m2＝2+5m+1，解得m＝3或m
（舍去），
∴aij＝ai13j﹣1＝[2+（i﹣1）×m]3j﹣1＝（3i﹣1）3j﹣1，
∴a67＝17×36，
∴S＝(a11+a12+a13+……+a1n)+(a21+a22+a23+……+a2n)+……+(an1＋an2＋an3＋……＋ann)
（3n﹣1）
n（3n+1）（3n﹣1）
故选：ACD.
【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网络外卖也开始成为不少人日常生活中不可或缺的一部分
市某调查机构针对该市市场占有率最高的两种网络外卖企业
以下简称外卖A、外卖
的服务质量进行了调查，从使用过这两种外卖服务的市民中随机抽取了1000人，每人分别对这两家外卖企业评分，满分均为100分，并将分数分成5组，得到以下频数分布表：
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高，说明市民对网络外卖服务越满意
若得分不低于60分，则表明该市民对网络外卖服务质量评价较高现将分数按“服务质量指标”划分成以下四个档次：
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率，解决下列问题：
从该市使用过外卖A的市民中任选5人，记对外卖A服务质量评价较高的人数为X，求X的数学期望．
从参与调查的市民中随机抽取1人，试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率；
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用，如果从这两种外卖的“服务质量指标”的期望角度看，他选择哪种外卖更合适？试说明理由．
