题目内容
已知数列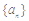 满足:
满足: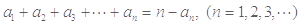
(1)求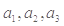 的值;
的值;
(2)求证:数列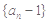 是等比数列;
是等比数列;
(3)令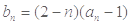 (
(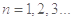 ),如果对任意
),如果对任意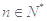 ,都有
,都有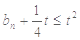 ,求实数
,求实数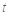 的取值范围.
的取值范围.
(1)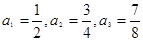 ;(2)
;(2)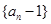 是以
是以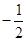 为首相
为首相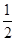 为公比的等比数列;
为公比的等比数列;
(3)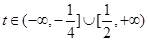
解析试题分析:(1)利用赋值法,令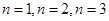 可求
可求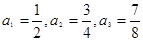 ;
;
(2)将等式写到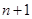 ,再将得到的式子与已知等式联立,两式再相减,根据等比数列的定
,再将得到的式子与已知等式联立,两式再相减,根据等比数列的定 ,可证明
,可证明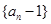 是以
是以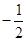 为首相
为首相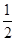 为公比的等比数列;
为公比的等比数列;
(3)由(2)可写出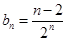 ,利用数列的单调性当
,利用数列的单调性当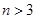 时,
时,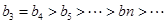 ,当
,当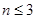 时,
时,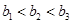 ,因此,数列
,因此,数列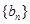 的最大值为
的最大值为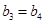 ,则
,则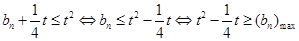 可解的
可解的 的范围.
的范围.
试题解析:(1)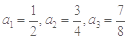
(2)由题可知: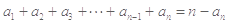 ①
①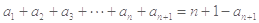 ②
②
②-①可得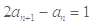 即:
即: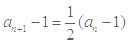 ,又
,又
∴数列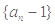 是以
是以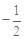 为首项,以
为首项,以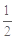 为公比的等比数列
为公比的等比数列
(3)由(2)可得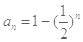 ,
, 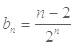
由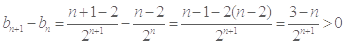 可得
可得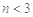
由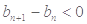 可得
可得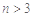 ,所以
,所以 
故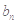 有最大值
有最大值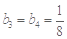
所以,对任意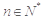 ,有
,有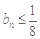
如果对任意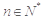 ,都有
,都有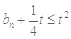 ,即
,即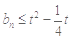 成立,
成立,
则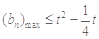 ,故有:
,故有: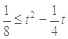 ,解得
,解得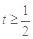 或
或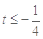
∴实数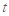 的取值范围是
的取值范围是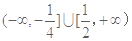
考点:1、赋值法求值;2、等比数列的定义;3、方程思想;4、数列的单调性、最值;5、恒成立问题、不等式.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 的前n项和, 求T2 013的值.
的前n项和, 求T2 013的值.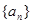 的首项为
的首项为 (
(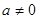 ),前
),前 项和为
项和为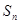 ,且
,且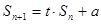 (
(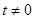 ).设
).设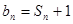 ,
, (
(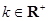 ).
).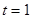 时,若对任意
时,若对任意 ,
,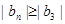 恒成立,求
恒成立,求 时,试求三个正数
时,试求三个正数 ,
, 的一组值,使得
的一组值,使得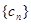 为等比数列,且
为等比数列,且 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数 的最大整数(如
的最大整数(如 ),记
),记 ,数列
,数列 项和为
项和为 ,数列
,数列 的前
的前 .
. ,求
,求 ;
; (
( )的充分必要条件为
)的充分必要条件为 ;
; 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
. ,求数列
,求数列 的前n项和.
的前n项和.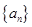 的前
的前 项和是
项和是 ,且
,且 .求数列
.求数列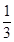 )是函数
)是函数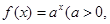 且
且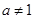 )的图象上一点,等比数列
)的图象上一点,等比数列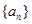 的前
的前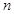 项和为
项和为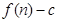 ,数列
,数列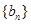
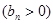 的首项为
的首项为 ,且前
,且前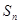 满足
满足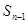 =
=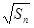 +
+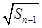 (
(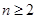 ).
).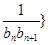 前
前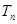 ,问
,问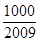 的最小正整数
的最小正整数 中,
中, ,
, .
. 满足
满足 ,数列
,数列 项和为
项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.