题目内容
对任意的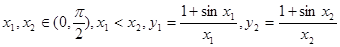 ,则( )
,则( )
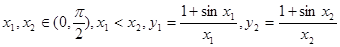 ,则( )
,则( )A. | B. |
C. | D. 的大小不能确定 的大小不能确定 |
A
试题分析:根据已知条件,对任意的
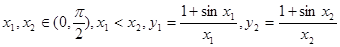 ,设函数
,设函数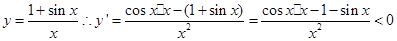 ,那么根据三角函数的有界性可知,原函数单调递减,因此可知
,那么根据三角函数的有界性可知,原函数单调递减,因此可知 ,选A.
,选A.点评:根据函数的解析式,确定大小关系的问题,就是要从函数的单调性的角度来分析和加以证明即可。同时要对于函数的构造这一点要合理构造,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
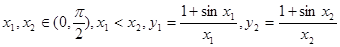 ,则( )
,则( )A. | B. |
C. | D. 的大小不能确定 的大小不能确定 |
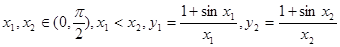 ,设函数
,设函数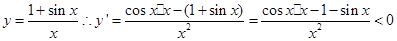 ,那么根据三角函数的有界性可知,原函数单调递减,因此可知
,那么根据三角函数的有界性可知,原函数单调递减,因此可知 ,选A.
,选A.
 名校课堂系列答案
名校课堂系列答案