题目内容
已知数列{an}满足a1=2,an+1=an-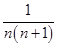 .
.
(1)求数列{an}的通项公式;
(2)设bn=nan·2n,求数列{bn}的前n项和Sn
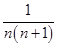 .
.(1)求数列{an}的通项公式;
(2)设bn=nan·2n,求数列{bn}的前n项和Sn
(1) an=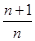 .(2) Sn=n·2n+1.
.(2) Sn=n·2n+1.
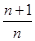 .(2) Sn=n·2n+1.
.(2) Sn=n·2n+1. 试题分析:(1)由已知得an+1-an=-
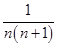 ,又a1=2,
,又a1=2,∴当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=
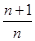 ,
,a1=2也符合上式,∴对一切n∈N*,an=
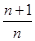 . 6分
. 6分(2)由(1)知:bn=nan·2n=(n+1)·2n,
∴Sn=2×2+3×22+4×23+…+(n+1)×2n,①
2Sn=2×22+3×23+…+n×2n+(n+1)×2n+1,②
∴①-②得-Sn=2×2+22+23+…+2n-(n+1)×2n+1=2+
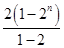 -(n+1)×2n+1
-(n+1)×2n+1=2+2n+1-2-(n+1)·2n+1=-n·2n+1,∴Sn=n·2n+1. 12分
点评:数列解答题考查的的热点为求数列的通项公式、等差(比)数列的性质及数列的求和问题.因此在复习中,要特别注意加强对由递推公式求通项公式、求有规律的非等差(比)数列的前n项和等的专项训练.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 满足
满足 ,若
,若 ,则
,则 的值为 .
的值为 .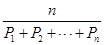 为
为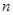 个正数
个正数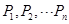 的“均倒数”.若数列
的“均倒数”.若数列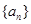 的前
的前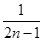 ,则数列
,则数列



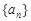 是公差为
是公差为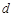 的等差数列,其前
的等差数列,其前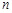 项和为
项和为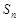 ,已知
,已知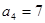 ,
,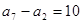 。
。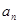 及前
及前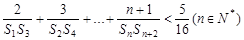 。
。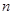 ,设曲线
,设曲线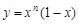 在
在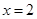 处的切线与
处的切线与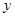 轴交点的纵坐标为
轴交点的纵坐标为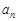 ,则数列
,则数列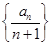 的前
的前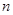 行有
行有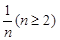 ,并且相邻两行数之间有一定的关系,则第8行第4个数为________
,并且相邻两行数之间有一定的关系,则第8行第4个数为________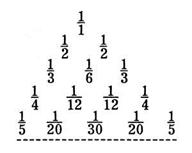
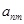 表示位于从上到下第
表示位于从上到下第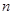 行,从左到右
行,从左到右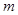 列的数 ,比如
列的数 ,比如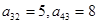 ,若
,若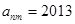 ,则有( )
,则有( )

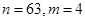


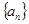 中,
中,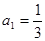 ,前
,前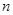 项和
项和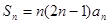 ,则数列
,则数列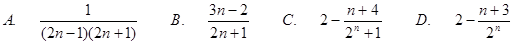
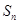 是等差数列
是等差数列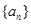 的前
的前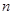 项和,且
项和,且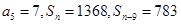 ,则
,则 。
。