题目内容
(本小题满分16分)对于函数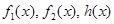 ,如果存在实数
,如果存在实数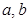 使得
使得
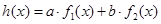 ,那么称
,那么称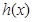 为
为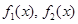 的生成函数.
的生成函数.
(Ⅰ)下面给出两组函数,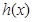 是否分别为
是否分别为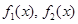 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: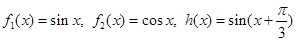 ;
;
第二组: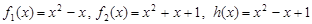 ;
;
(Ⅱ)设 ,生成函数
,生成函数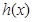 .若不等式
.若不等式
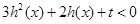 在
在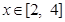 上有解,求实数
上有解,求实数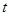 的取值范围;
的取值范围;
(Ⅲ)设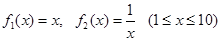 ,取
,取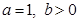 ,生成函数
,生成函数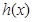 使
使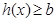 恒成立,求
恒成立,求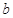 的取值范围.
的取值范围.
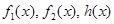 ,如果存在实数
,如果存在实数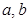 使得
使得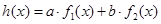 ,那么称
,那么称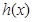 为
为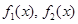 的生成函数.
的生成函数.(Ⅰ)下面给出两组函数,
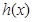 是否分别为
是否分别为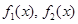 的生成函数?并说明理由;
的生成函数?并说明理由;第一组:
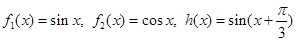 ;
;第二组:
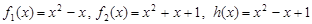 ;
;(Ⅱ)设
 ,生成函数
,生成函数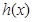 .若不等式
.若不等式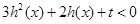 在
在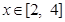 上有解,求实数
上有解,求实数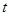 的取值范围;
的取值范围;(Ⅲ)设
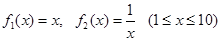 ,取
,取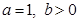 ,生成函数
,生成函数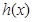 使
使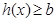 恒成立,求
恒成立,求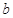 的取值范围.
的取值范围.解:(Ⅰ)① 设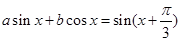 ,即
,即
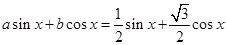 ,取
,取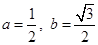 ,所以
,所以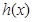 是
是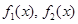 的生成函数.……………………2分
的生成函数.……………………2分
② 设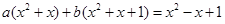 ,即
,即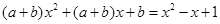 ,
,
则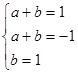 ,该方程组无解.所以
,该方程组无解.所以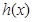 不是
不是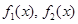 的生成函数.………4分
的生成函数.………4分
(Ⅱ)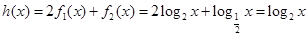 …………………………5分
…………………………5分
若不等式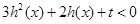 在
在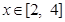 上有解,
上有解,
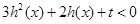 ,即
,即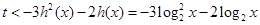 ……7分
……7分
设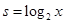 ,则
,则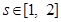 ,
,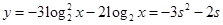 ,……9分
,……9分
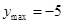 ,故,
,故,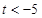 .………………………………………………………10分
.………………………………………………………10分
(Ⅲ)由题意,得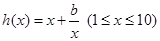
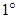 若
若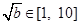 ,则
,则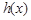 在
在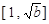 上递减,在
上递减,在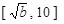 上递增,
上递增,
则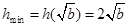 ,所以
,所以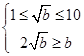 ,得
,得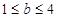 …………12分
…………12分
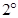 若
若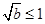 ,则
,则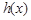 在
在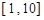 上递增,则
上递增,则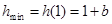 ,
,
所以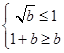 ,得
,得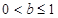 .………………………………………………14分
.………………………………………………14分
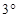 若
若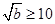 ,则
,则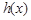 在
在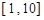 上递减,则
上递减,则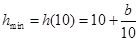 ,故
,故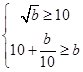 ,无解
,无解
综上可知,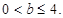 ………………………………………………………16分
………………………………………………………16分
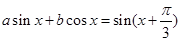 ,即
,即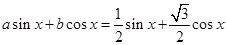 ,取
,取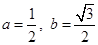 ,所以
,所以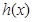 是
是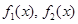 的生成函数.……………………2分
的生成函数.……………………2分② 设
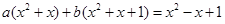 ,即
,即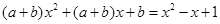 ,
,则
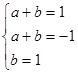 ,该方程组无解.所以
,该方程组无解.所以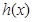 不是
不是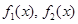 的生成函数.………4分
的生成函数.………4分(Ⅱ)
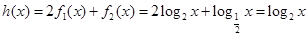 …………………………5分
…………………………5分若不等式
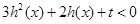 在
在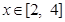 上有解,
上有解,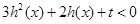 ,即
,即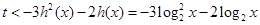 ……7分
……7分设
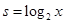 ,则
,则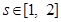 ,
,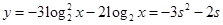 ,……9分
,……9分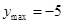 ,故,
,故,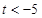 .………………………………………………………10分
.………………………………………………………10分(Ⅲ)由题意,得
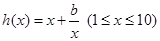
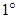 若
若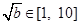 ,则
,则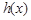 在
在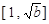 上递减,在
上递减,在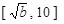 上递增,
上递增,则
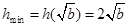 ,所以
,所以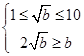 ,得
,得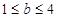 …………12分
…………12分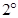 若
若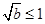 ,则
,则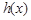 在
在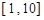 上递增,则
上递增,则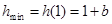 ,
,所以
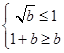 ,得
,得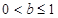 .………………………………………………14分
.………………………………………………14分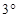 若
若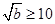 ,则
,则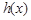 在
在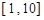 上递减,则
上递减,则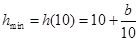 ,故
,故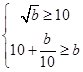 ,无解
,无解综上可知,
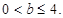 ………………………………………………………16分
………………………………………………………16分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 且
且 的图象上存在不同两点
的图象上存在不同两点 ,且
,且 的取值范围是
的取值范围是 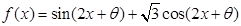 的图像关于原点对称,且满足对于
的图像关于原点对称,且满足对于 内任意两个数
内任意两个数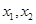 ,恒有
,恒有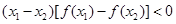 的
的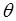 的一个取值可以是( )
的一个取值可以是( )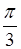 B.
B.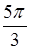 C.
C.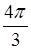 D.
D.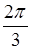
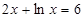 的解为
的解为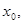 则
则 所在的区间是( )
所在的区间是( )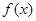 的定义域为
的定义域为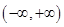 ,
,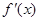 为
为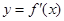 的图象如图所示,且
的图象如图所示,且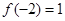 ,
,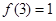 ,则不等式
,则不等式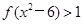 的解集为( )
的解集为( )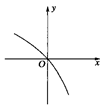
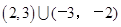
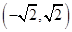
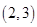
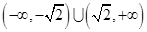
 上的函数
上的函数 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 .
. 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上的有界函数,且
上的有界函数,且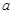 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界
上的上界 的取值范围.
的取值范围. 若有
若有 则
则 的取值范围为( )
的取值范围为( )


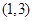
 ,
, ,
, ,则由表中数据确定
,则由表中数据确定 、
、 、
、 依次对应 ( ).
依次对应 ( ). 、
、 、
、
