题目内容
.设函数f(x)=-a+x+a,x∈(0,1],a∈R*.
(1)若f(x)在(0,1]上是增函数,求a的取值范围;
(2)求f(x)在(0,1]上的最大值.
(1)若f(x)在(0,1]上是增函数,求a的取值范围;
(2)求f(x)在(0,1]上的最大值.
(1)由f(x)在(0,1]上为增函数,知f′(x)≥0在(0,1]上恒成立,即a≤在(0,1]上恒成立,故a只需小于或等于在(0,1]上的最小值.
(2)求f(x)在(0,1]上的最大值时由(1)的结论可对a分类讨论,分0<a≤及a>两种情况,当0<a≤时,由(1)知f(x)在(0,1]上为增函数,可求最大值,当a>时,可由导数求f(x)在(0,1]上的极大值点.
[解析] (1)f′(x)=-a·+1.
因为f(x)在(0,1]上是增函数,
所以f′(x)=-+1≥0在(0,1]上恒成立,
即a≤=在(0,1]上恒成立,
而在(0,1]上的最小值为,
又因为a∈R*,所以0<a≤.
(2)由(1)知:①当0<a≤时,f(x)在(0,1]上是增函数,所以f(x)max=f(1)=(1-)a+1;
②当a>时,令f′(x)=0,得x=∈(0,1],
因为当0<x<时,f′(x)>0,
当<x≤1时,f′(x)<0,
所以f(x)在点x=处取得极大值,
即为f=+a
=+a=a-,
故f(x)max=a-.
综上,当0<a≤时,f(x)max=(1-)a+1;
当a>时,f(x)max=a-.
[点评] ①已知f(x)在[a,b]上单调递增(或单调递减)可推得x∈[a,b]时,f′(x)≥0(或f′(x)≤0)恒成立,求单调区间时,令f′(x)>0(或f′(x)<0).②求f(x)的最大值时,要比较端点处函数值与极值的大小.当f′(x)的符号不确定时,可对待定系数进行分类讨论.
略

练习册系列答案
相关题目
 满足
满足
 的值并求出相应的
的值并求出相应的 的解析式
的解析式 ,使得
,使得
 ]?若存在,求出
]?若存在,求出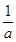 -
-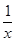 (a>0,x>0).
(a>0,x>0).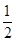 ,2]上的值域是[
,2]上的值域是[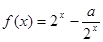 (
(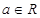 ),将
),将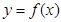 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数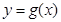 的图象,函数
的图象,函数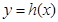 与函数
与函数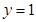 对称.
对称.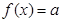 在
在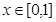 上有且仅有一个实根,求
上有且仅有一个实根,求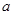 的取值范围;
的取值范围; ,已知
,已知 对任意的
对任意的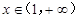 恒成立,求
恒成立,求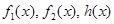 ,如果存在实数
,如果存在实数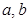 使得
使得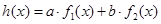 ,那么称
,那么称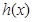 为
为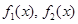 的生成函数.
的生成函数.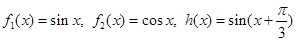 ;
;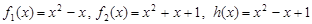 ;
; ,生成函数
,生成函数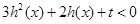 在
在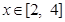 上有解,求实数
上有解,求实数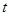 的取值范围;
的取值范围;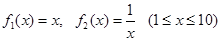 ,取
,取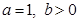 ,生成函数
,生成函数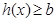 恒成立,求
恒成立,求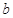 的取值范围.
的取值范围. (百万元)广告费,增加的销售额可近似的用函数
(百万元)广告费,增加的销售额可近似的用函数 (百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数
(百万元)来计算;每投入x(百万元)技术改造费用,增加的销售额可近似的用函数 (百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)
(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:≈1.41,≈1.73)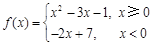 ,若
,若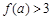 ,则实数
,则实数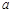 的取值范围是 ▲ .
的取值范围是 ▲ .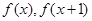 均是定义域为
均是定义域为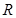 的偶函数,且
的偶函数,且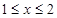 时,
时,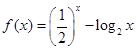 ,则
,则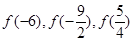 的大小关系为
的大小关系为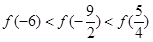
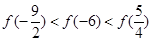
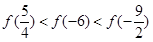
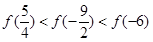
 ,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )
,其中Pn为预测人口数,P0为初期人口数,k为预测年内增长率,n为预测期间隔年数.如果在某一时期有-1<k<0,那么这期间人口数 ( )