题目内容
已知圆 的圆心在点
的圆心在点 ,点
,点 ,求;
,求;
(1)过点 的圆的切线方程;
的圆的切线方程;
(2) 点是坐标原点,连结
点是坐标原点,连结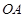 ,
, ,求
,求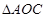 的面积
的面积 .
.
(1)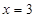 或
或 ;(2)
;(2) .
.
解析试题分析:(1)过圆外一点作圆的切线,一定是有两条切线,而求切线方程我们一般是用点斜式写出直线方程,再利用圆心到切线的距离等于圆的半径列出方程求出切线斜率 ,这时可能会出现只有一解的情形,事实上这种情况的出现,一般是另一条切线斜率不存在,即切线与
,这时可能会出现只有一解的情形,事实上这种情况的出现,一般是另一条切线斜率不存在,即切线与 轴垂直,不有忘记.(2)已知三角形三个顶点坐标,要求三角形的面积,可以采取直接的一边长如
轴垂直,不有忘记.(2)已知三角形三个顶点坐标,要求三角形的面积,可以采取直接的一边长如 ,再求出AC边长的高即点O到直线AC的距离在
,再求出AC边长的高即点O到直线AC的距离在 在,即能求出面积.当然也可用图形的切割来求面积,计算如下:
在,即能求出面积.当然也可用图形的切割来求面积,计算如下: .请读者体会一下,为什么可以这么做?
.请读者体会一下,为什么可以这么做?
试题解析:(1) (1分)
(1分)
当切线的斜率不存在时,对于直线 到直线的距离为1,满足条件(3分)
到直线的距离为1,满足条件(3分)
当 存在时,设直线
存在时,设直线 ,即
,即 ,
,
得 (5分)
(5分)
∴得直线方程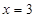 或
或 (6分)
(6分)
(2) (7分)
(7分) (8分)
(8分) (10分)
(10分) (12分)
(12分)
考点:(1)圆的切线;(2)三角形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为 为参数),圆
为参数),圆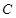 的极坐标方程为
的极坐标方程为 .
. 对称,求
对称,求 的值;
的值; 到定点
到定点 与到定点
与到定点 的距离之比为
的距离之比为 .
. 的轨迹C的方程,并指明曲线C的轨迹;
的轨迹C的方程,并指明曲线C的轨迹; ,若曲线C上恰有三个点到直线
,若曲线C上恰有三个点到直线 的距离为1,求实数
的距离为1,求实数 的值。
的值。 ,直线
,直线 .
. 与圆C的位置关系;
与圆C的位置关系; ,求此时直线
,求此时直线 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆 与
与 轴的另一个交点为
轴的另一个交点为 .
. 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
. 为圆心的圆与
为圆心的圆与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,其中
,其中 为坐标原点。
为坐标原点。 的面积为定值;
的面积为定值; 与圆
与圆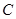 交于点
交于点 ,若
,若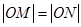 ,求圆
,求圆 在极坐标系中的方程为
在极坐标系中的方程为 ,圆C在极坐标系中的方程为
,圆C在极坐标系中的方程为 ,求圆C被直线
,求圆C被直线 经过点
经过点 ,且和圆
,且和圆 相交,截得的弦长为4
相交,截得的弦长为4 ,求直线
,求直线