题目内容
已知以点 为圆心的圆与
为圆心的圆与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,其中
,其中 为坐标原点。
为坐标原点。
(1)求证: 的面积为定值;
的面积为定值;
(2)设直线 与圆
与圆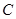 交于点
交于点 ,若
,若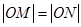 ,求圆
,求圆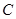 的方程。
的方程。
(1)4;(2)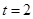 ,
,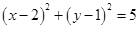
解析试题分析:(1)因为,圆与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,所以,
,所以,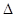 OAB是直角三角,又圆心
OAB是直角三角,又圆心 ,所以
,所以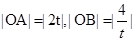 ,
, 的面积为
的面积为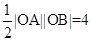 为定值。
为定值。
(2)直线 与圆
与圆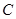 交于点
交于点 ,且
,且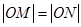 ,所以,MN的中垂线是OC,OC斜率
,所以,MN的中垂线是OC,OC斜率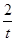 ,由
,由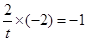 ,得t=2,则C(2,1),OC即圆半径其长为
,得t=2,则C(2,1),OC即圆半径其长为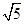 。
。
故圆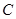 的方程是
的方程是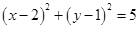 。
。
考点:直线方程,直线与圆的位置关系,圆的方程。
点评:中档题,确定圆的方程,常常应用“待定系数法”。本题充分利用图形的几何性质,从确定圆心、半径入手,得到圆的方程。

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 作圆
作圆 .
.
 三点共线;
三点共线; .
.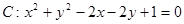 ,直线
,直线  ,
, 与圆
与圆 交与
交与 两点,点
两点,点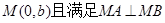 .
. 时,求
时,求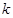 的值;
的值;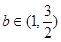 时,求
时,求 的圆心在点
的圆心在点 ,点
,点 ,求;
,求; 的圆的切线方程;
的圆的切线方程; 点是坐标原点,连结
点是坐标原点,连结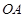 ,
, ,求
,求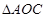 的面积
的面积 .
. 与直线l:
与直线l: ,且直线l被圆C截得的弦长为
,且直线l被圆C截得的弦长为 .
.  的值;
的值;  时,求过点(3,5)且与圆C相切的直线方程.
时,求过点(3,5)且与圆C相切的直线方程. 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为,圆心在上.
的半径为,圆心在上.
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心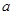 的取值范围.
的取值范围.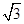 ,半径小于5.
,半径小于5. 和圆
和圆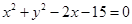 相交于点
相交于点 。
。 的垂直平分线方程;(2)求弦
的垂直平分线方程;(2)求弦 中,直线
中,直线 截以原点
截以原点 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为
 与圆
与圆 ,当
,当 长最小时,求直线
长最小时,求直线 的直线
的直线 ,使
,使 ,以
,以