题目内容
在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为 为参数),圆
为参数),圆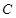 的极坐标方程为
的极坐标方程为 .
.
(1)若圆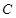 关于直线
关于直线 对称,求
对称,求 的值;
的值;
(2)若圆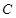 与直线
与直线 相切,求
相切,求 的值.
的值.
(1)2;(2)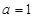 或
或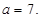
解析试题分析:(1)因为要求圆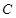 关于直线
关于直线 对称的圆,首先将直线的参数方程化为普通方程,同样的要将圆的极坐标方程化为普通方程,由于圆关于直线对称,所以直线经过圆的圆心.所以将圆心的坐标代入直线方程即可求出结论.
对称的圆,首先将直线的参数方程化为普通方程,同样的要将圆的极坐标方程化为普通方程,由于圆关于直线对称,所以直线经过圆的圆心.所以将圆心的坐标代入直线方程即可求出结论.
(2)若圆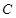 与直线
与直线 相切,则圆心到直线的距离为半径的长,由(1)可得的直线方程和圆的方程可得相应的量,从而可求出结论.
相切,则圆心到直线的距离为半径的长,由(1)可得的直线方程和圆的方程可得相应的量,从而可求出结论.
试题解析:(1) 直线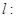
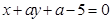 ;
;
圆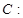
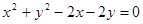 ,圆心为
,圆心为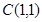 ,半径
,半径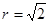 .由题设知,直线
.由题设知,直线 过圆心,所以
过圆心,所以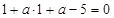 ,所以
,所以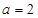 ;
;
(2)点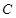 到直线
到直线 的距离为
的距离为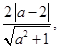 因此
因此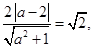
整理得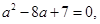 ,所以
,所以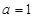 或
或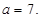
考点:1.直线的参数方程.2.圆的极坐标方程.3.直线与圆的位置关系.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点. 的方程:
的方程: ,其中
,其中 .
. 相交于
相交于 ,
, 两点,且
两点,且 ,求
,求 的值;
的值; ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由.
的范围,若不存在,说明理由. :
: 和圆
和圆 :
:

 ,求直线l的方程;
,求直线l的方程; 和
和 ,它们分别与圆
,它们分别与圆 与圆
与圆 外切于点
外切于点 ,直线
,直线 是两圆的外公切线,分别与两圆相切于
是两圆的外公切线,分别与两圆相切于 两点,
两点, 是圆
是圆 作圆
作圆 .
.
 三点共线;
三点共线; .
.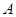 (-1,1),
(-1,1), (1,3).
(1,3). 两点的直线方程;
两点的直线方程; 轴上的圆的方程.
轴上的圆的方程. 的圆心在点
的圆心在点 ,点
,点 ,求;
,求; 的圆的切线方程;
的圆的切线方程; 点是坐标原点,连结
点是坐标原点,连结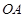 ,
, ,求
,求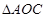 的面积
的面积 .
.