题目内容
(本题满分15分)如图,已知 的三边长分别为
的三边长分别为 ,以点
,以点 为圆心,
为圆心, 为半径作一个圆.
为半径作一个圆.
(1) 求 的面积;
的面积;
(2)设 为
为 的任意一条直径,记
的任意一条直径,记 ,求
,求 的最大值和最小值,并说明当
的最大值和最小值,并说明当 取最大值和最小值时,
取最大值和最小值时, 的位置特征是什么?
的位置特征是什么?
 的三边长分别为
的三边长分别为 ,以点
,以点 为圆心,
为圆心, 为半径作一个圆.
为半径作一个圆.(1) 求
 的面积;
的面积;(2)设
 为
为 的任意一条直径,记
的任意一条直径,记 ,求
,求 的最大值和最小值,并说明当
的最大值和最小值,并说明当 取最大值和最小值时,
取最大值和最小值时, 的位置特征是什么?
的位置特征是什么?(1)
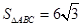 (2)
(2) 的最大值为22,最小值为-6,取最值时
的最大值为22,最小值为-6,取最值时


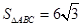 (2)
(2) 的最大值为22,最小值为-6,取最值时
的最大值为22,最小值为-6,取最值时

本试题主要是考查了向量的数量积公式,以及解三角形的面积公式,和余弦定理的综合运用。
(1)利用已知的边可以运用余弦定理得到其中的一个角,然后借助于正弦面积公式得到三角形的面积。
(2)将所求的向量化为 ,然后借助于向量的数量积公式化简得到关于角的三角函数从而得到最值。
,然后借助于向量的数量积公式化简得到关于角的三角函数从而得到最值。
解:1)
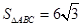
2)

(其中 为
为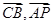 的夹角)
的夹角)
 的最大值为22,最小值为-6,取最值时
的最大值为22,最小值为-6,取最值时
(1)利用已知的边可以运用余弦定理得到其中的一个角,然后借助于正弦面积公式得到三角形的面积。
(2)将所求的向量化为
 ,然后借助于向量的数量积公式化简得到关于角的三角函数从而得到最值。
,然后借助于向量的数量积公式化简得到关于角的三角函数从而得到最值。解:1)

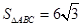
2)


(其中
 为
为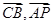 的夹角)
的夹角) 的最大值为22,最小值为-6,取最值时
的最大值为22,最小值为-6,取最值时

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
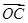 =
=
 +
+
 ,其中
,其中

 向量
向量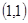 向上向左均平移1个单位后所得向量为 ;
向上向左均平移1个单位后所得向量为 ;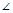 A=90°,AB=1,设点P,Q满足
A=90°,AB=1,设点P,Q满足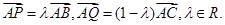 若
若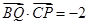 ,则
,则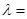



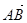 ·
·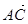 =-2,则|
=-2,则|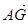 |的最小值是 .
|的最小值是 .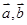 夹角为
夹角为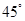 ,且
,且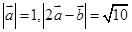 ;则
;则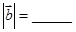
 ,
, ,
, 满足
满足 ,且
,且 ,则
,则 ,则
,则 =
=

 ,
, ,
, ,
, ,则
,则 。(用
。(用 表示)
表示)