题目内容
求适合下列条件的双曲线的标准方程
(Ⅰ)求以椭圆
+
=1的焦点为焦点,以直线y=±
x为渐近线
(Ⅱ)双曲线的两条对称轴是坐标轴,实轴长是虚轴长的一半,且过点(3,2)
(Ⅰ)求以椭圆
| x2 |
| 13 |
| y2 |
| 3 |
| 1 |
| 2 |
(Ⅱ)双曲线的两条对称轴是坐标轴,实轴长是虚轴长的一半,且过点(3,2)
(I)由椭圆
+
=1可得c=
=
,得到焦点(±
,0).
设双曲线的标准方程为
-
=1(a>0,b>0),∴a2+b2=(
)2=10.
又
=
.联立
,解得
.
因此所求的双曲线的方程为:
-
=1.
(II)由题意可知:焦点在x轴上,
设双曲线的标准方程为
-
=1(a>0,b>0),
∵实轴长是虚轴长的一半,且过点(3,2).
∴
,解得
,
∴双曲线的标准方程为
-
=1.
| x2 |
| 13 |
| y2 |
| 3 |
| 13-3 |
| 10 |
| 10 |
设双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
又
| b |
| a |
| 1 |
| 2 |
|
|
因此所求的双曲线的方程为:
| x2 |
| 8 |
| y2 |
| 2 |
(II)由题意可知:焦点在x轴上,
设双曲线的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵实轴长是虚轴长的一半,且过点(3,2).
∴
|
|
∴双曲线的标准方程为
| x2 |
| 8 |
| y2 |
| 32 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
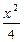 -
-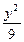 =1的渐近线方程是
=1的渐近线方程是 y=±
y=±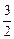 x B
x B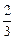 x C
x C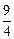 x D
x D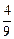 x
x