题目内容
4.已知|${\overrightarrow{OA}}$|=2,|${\overrightarrow{OB}}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,点C在AB上,∠AOC=30°.则向量$\overrightarrow{OC}$等于( )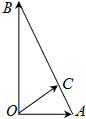
| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
分析 过点C做CE∥OA,CF∥OB,得到两个三角形相似,根据三角形相似得到对应边成比例,把OE,OF都用OC来表示,代入比例式,求出OC的值,做出向量之间的关系.
解答 解:过点C做CE∥OA,CF∥OB
设OC长度为a
有△CEB∽△AFC
∴$\frac{BE}{CF}$=$\frac{CE}{AF}$ ①
∵∠AOC=30°
则CF=$\frac{1}{2}$a=OE
OF=CE=$\frac{\sqrt{3}}{2}$a,
∴BE=2-$\frac{1}{2}$a AF=2-$\frac{\sqrt{3}}{2}$a,
代入①中化简整理可解:a=$\sqrt{3}$,
OF=$\frac{\sqrt{3}a}{2}$=$\frac{3}{2}$=$\frac{3}{4}$OA,OE=$\frac{a}{2}$=$\frac{\sqrt{3}}{2}$=$\frac{1}{4}$OB,
∴$\overrightarrow{OC}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$,
故选:B.
点评 本题考查平面向量基本定理及其意义,本题解题的关键是构造平行四边形,利用平行四边形法则来解题,本题是一个易错题

练习册系列答案
相关题目
15.已知函数f(x)=$\frac{sinx}{|cosx|}$,则函数f(x)的最小正周期是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
12.已知点P(x,y)在曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}\right.$(θ为参数,且θ∈[π,2π))上,则点P到直线$\left\{\begin{array}{l}x=2+t\\ y=-1-t\end{array}\right.(t$为参数)的距离的取值范围是( )
| A. | [-$\frac{{3\sqrt{2}}}{2}$,$\frac{{3\sqrt{2}}}{2}$] | B. | [$\frac{{3\sqrt{2}}}{2}$-1,$\frac{{3\sqrt{2}}}{2}$+1] | C. | ($\sqrt{2}$,2$\sqrt{2}$] | D. | ($\sqrt{2}$,$\frac{{3\sqrt{2}}}{2}$+1] |
14.已知命题p函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+x有两个极值点;命题q:函数g(x)=x${\;}^{{a}^{2}-a}$在(0,+∞)上为增函数,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |