题目内容
13.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$下,目标函数z=x+my取得最大值z(m)的实数对(x,y)=($\frac{1}{m+1}$,$\frac{m}{m+1}$);而当m变化时,z(m)的取值范围是(1,+∞).分析 根据m>1,可以判断直线y=mx的倾斜角位于区间($\frac{π}{4}$,$\frac{π}{2}$)上,由此判断出满足约束条件的平面区域的形状,再根据目标函数z=x+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此可得关于m的函数表达式,根据函数的单调性,求出m的范围.
解答 解:∵m>1,由约束条件,作出可行域如图,
直线y=mx与直线x+y=1交于($\frac{1}{m+1}$,$\frac{m}{m+1}$),
目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1}$,$\frac{m}{m+1}$)处取得最大值,
∴Z(m)=$\frac{1{+m}^{2}}{1+m}$,则z′(m)=$\frac{{(m+1)}^{2}-2}{{(m+1)}^{2}}$,
∵m>1,∴z′(m)>0,
∴函数z(m)在(1,+∞)上单调递增,
∴z(m)最小值>z(1)=1,
故答案为:($\frac{1}{m+1}$,$\frac{m}{m+1}$),(1,+∞).
点评 题考查的知识点是简单线性规划的应用,其中根据平面直线方程判断出目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1}$,$\frac{m}{m+1}$)点取得最大值,并由此列出关于m的函数表达式是解答本题的关键,是中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.执行如图所示的程序框图,若输入x=30,则输出的结果为( )
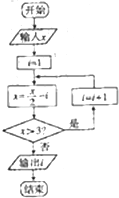

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
4.已知|${\overrightarrow{OA}}$|=2,|${\overrightarrow{OB}}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,点C在AB上,∠AOC=30°.则向量$\overrightarrow{OC}$等于( )
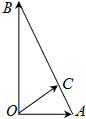

| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
8.已知θ∈R,则“θ=$\frac{π}{6}$”是“cosθ=$\frac{\sqrt{3}}{2}$”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
18.能够把椭圆$\frac{{x}^{2}}{4}$+y2=1的周长和面积同时分为相等的两部分的函数称为椭圆的“可分函数”,下列函数不是椭圆的“可分函数”为( )
| A. | f(x)=4x3+x | B. | f(x)=ln$\frac{5-x}{5+x}$ | C. | f(x)=sin$\frac{x}{2}$ | D. | f(x)=ex+e-x |
5.设实数x,y满足条件$\left\{\begin{array}{l}{4x-y-10≤0}\\{x-2y+8≥0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为12,则$\frac{8a+3b+2ab}{ab}$的最小值为( )
| A. | 12 | B. | $\frac{21}{3}$ | C. | $\frac{67}{6}$ | D. | 11 |
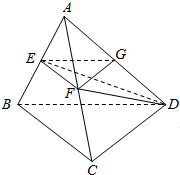 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证: