题目内容
16.以知f(x)是定义在区间[-1,1]上的奇函数,当x<0时,f(x)=x(x-1),则关于m的不等式f(1-m)+f(1-m2)<0的解集为[0,1).分析 根据函数奇偶性的性质将不等式进行转化即可.
解答 解:由题意,奇函数f(x)是定义在[-1,1]上的减函数,不等式f(1-m)+f(1-m2)<0,
即f(1-m)<f(m2-1),
则$\left\{\begin{array}{l}{-1≤1-m≤1}\\{-1≤1-{m}^{2}≤1}\\{1-m>{m}^{2}-1}\end{array}\right.$,即$\left\{\begin{array}{l}{0≤m≤2}\\{-\sqrt{2}≤m≤\sqrt{2}}\\{-2<m<1}\end{array}\right.$,
解得0≤m<1,
即m∈[0,1).
故答案为:[0,1).
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
6.某市教育局邀请教育专家深入该市多所中小学,开展听课、访谈及随堂检测等活动.他们把收集到的180节课分为三类课堂教学模式:教师主讲的为A模式,少数学生参与的为B模式,多数学生参与的为C模式.A、B、C三类课的节数比例为3:2:1
(Ⅰ)为便于研究分析,教育专家将A模式称为传统课堂模式,B、C统称为新课堂模式,根据随堂检测结果,把课堂教学效率分为高效和非高效,根据检测结果统计得到如下2×2列联表(单位:节)
请根据统计数据回答:有没有99%的把握认为课堂教学效率与教学模式有关?并说明理由.
(Ⅱ)教育专家采用分层抽样的方法从收集到的180节课中选出18节课作为样本进行研究,并从样本的B模式和C模式课堂中随机抽取3节课.
①求至少有一节为C模式课堂的概率;
②设随机抽取的3节课中含有C模式课堂的节数为X,求X的分布列和数学期望.
参考临界值表:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n =a +b +c +d
(Ⅰ)为便于研究分析,教育专家将A模式称为传统课堂模式,B、C统称为新课堂模式,根据随堂检测结果,把课堂教学效率分为高效和非高效,根据检测结果统计得到如下2×2列联表(单位:节)
| 高效 | 非高效 | 统计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 统计 | 100 | 80 | 180 |
(Ⅱ)教育专家采用分层抽样的方法从收集到的180节课中选出18节课作为样本进行研究,并从样本的B模式和C模式课堂中随机抽取3节课.
①求至少有一节为C模式课堂的概率;
②设随机抽取的3节课中含有C模式课堂的节数为X,求X的分布列和数学期望.
参考临界值表:
| P(K2≧K0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
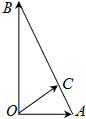
4.已知|${\overrightarrow{OA}}$|=2,|${\overrightarrow{OB}}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,点C在AB上,∠AOC=30°.则向量$\overrightarrow{OC}$等于( )

| A. | $\frac{1}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}$ | B. | $\frac{3}{4}\overrightarrow{OA}+\frac{1}{4}\overrightarrow{OB}$ | C. | $\frac{3}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ | D. | $\frac{5}{4}\overrightarrow{OA}-\frac{1}{4}\overrightarrow{OB}$ |
8.已知θ∈R,则“θ=$\frac{π}{6}$”是“cosθ=$\frac{\sqrt{3}}{2}$”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
5.设实数x,y满足条件$\left\{\begin{array}{l}{4x-y-10≤0}\\{x-2y+8≥0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为12,则$\frac{8a+3b+2ab}{ab}$的最小值为( )
| A. | 12 | B. | $\frac{21}{3}$ | C. | $\frac{67}{6}$ | D. | 11 |
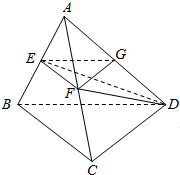 如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证:
如图,在四面体ABCD中,AD=BD,∠ABC=90°,点E,F分别为棱AB,AC上的点,点G为棱AD的中点,且平面EFG∥平面BCD.求证: