题目内容
已知函数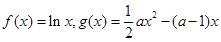 ,(
,(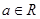 ).
).
(Ⅰ)已知函数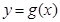 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数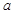 的范围.
的范围.
(Ⅱ)记函数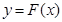 的图象为曲线
的图象为曲线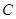 .设点
.设点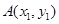 ,
,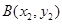 是曲线
是曲线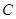 上的不同两点.如果在曲线
上的不同两点.如果在曲线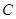 上存在点
上存在点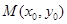 ,使得:①
,使得:①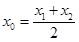 ;②曲线
;②曲线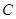 在点
在点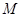 处的切线平行于直线
处的切线平行于直线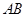 ,则称函数
,则称函数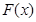 存在“中值相依切线”.
存在“中值相依切线”.
试问:函数 (
(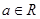 且
且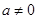 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由.
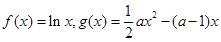 ,(
,(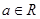 ).
).(Ⅰ)已知函数
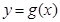 的零点至少有一个在原点右侧,求实数
的零点至少有一个在原点右侧,求实数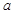 的范围.
的范围.(Ⅱ)记函数
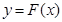 的图象为曲线
的图象为曲线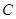 .设点
.设点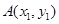 ,
,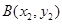 是曲线
是曲线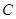 上的不同两点.如果在曲线
上的不同两点.如果在曲线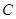 上存在点
上存在点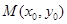 ,使得:①
,使得:①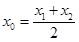 ;②曲线
;②曲线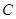 在点
在点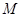 处的切线平行于直线
处的切线平行于直线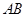 ,则称函数
,则称函数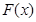 存在“中值相依切线”.
存在“中值相依切线”.试问:函数
 (
(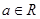 且
且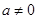 )是否存在“中值相依切线”,请说明理由.
)是否存在“中值相依切线”,请说明理由. (Ⅰ)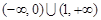 (Ⅱ)函数
(Ⅱ)函数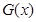 不存在“中值相依切线”,理由见解析。
不存在“中值相依切线”,理由见解析。
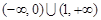 (Ⅱ)函数
(Ⅱ)函数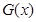 不存在“中值相依切线”,理由见解析。
不存在“中值相依切线”,理由见解析。解:(Ⅰ)(1)当 时,
时, ,直线与
,直线与 轴的交点为
轴的交点为 ,即函数
,即函数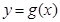 的零点为0,不在原点右侧,不满足条件. (1分)
的零点为0,不在原点右侧,不满足条件. (1分)
(2)当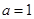 时,
时, ,抛物线的顶点为
,抛物线的顶点为 ,即函数
,即函数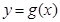 的零点为0,不在原点右侧,不满足条件. (2分)
的零点为0,不在原点右侧,不满足条件. (2分)
(3)当 时,
时,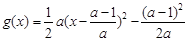 ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴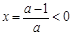 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的左侧,故函数
轴的另一交点在对称轴的左侧,故函数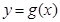 的零点不在原点右侧,不满足条件. (3分)
的零点不在原点右侧,不满足条件. (3分)
(4)当 时,
时, ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的右侧,故函数
轴的另一交点在对称轴的右侧,故函数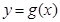 有一个零点在原点右侧,满足条件. (4分)
有一个零点在原点右侧,满足条件. (4分)
(5)当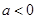 时,
时, ,抛物线开口向下且过原点,对称轴
,抛物线开口向下且过原点,对称轴 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的右侧,故函数
轴的另一交点在对称轴的右侧,故函数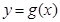 有一个零点在原点右侧,满足条件. (5分)
有一个零点在原点右侧,满足条件. (5分)
综上可得,实数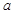 的取值范围是
的取值范围是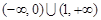 . (6分)
. (6分)
(Ⅱ)假设函数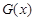 存在“中值相依切线”.
存在“中值相依切线”.
设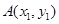 ,
,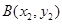 是曲线
是曲线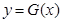 上的不同两点,且
上的不同两点,且 ,
,
则 ,
,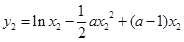 .
.


 (8分)
(8分)
曲线在点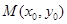 处的切线斜率
处的切线斜率


 , (9分)
, (9分)
依题意得:
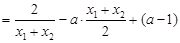 .
.
化简可得: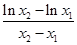
 , 即
, 即 =
=
 . (11分)
. (11分)
设 (
(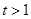 ),上式化为:
),上式化为: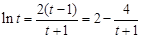 , 即
, 即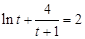 . (12分)
. (12分)
令 ,
,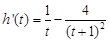
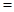
 .
.
因为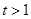 ,显然
,显然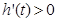 ,所以
,所以 在
在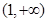 上递增,显然有
上递增,显然有 恒成立.
恒成立.
所以在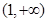 内不存在
内不存在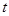 ,使得
,使得 成立.
成立.
综上所述,假设不成立.所以,函数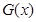 不存在“中值相依切线”. (14分)
不存在“中值相依切线”. (14分)
 时,
时, ,直线与
,直线与 轴的交点为
轴的交点为 ,即函数
,即函数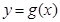 的零点为0,不在原点右侧,不满足条件. (1分)
的零点为0,不在原点右侧,不满足条件. (1分)(2)当
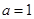 时,
时, ,抛物线的顶点为
,抛物线的顶点为 ,即函数
,即函数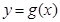 的零点为0,不在原点右侧,不满足条件. (2分)
的零点为0,不在原点右侧,不满足条件. (2分)(3)当
 时,
时,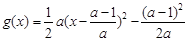 ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴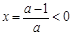 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的左侧,故函数
轴的另一交点在对称轴的左侧,故函数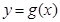 的零点不在原点右侧,不满足条件. (3分)
的零点不在原点右侧,不满足条件. (3分)(4)当
 时,
时, ,抛物线开口向上且过原点,对称轴
,抛物线开口向上且过原点,对称轴 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的右侧,故函数
轴的另一交点在对称轴的右侧,故函数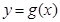 有一个零点在原点右侧,满足条件. (4分)
有一个零点在原点右侧,满足条件. (4分)(5)当
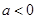 时,
时, ,抛物线开口向下且过原点,对称轴
,抛物线开口向下且过原点,对称轴 ,所以抛物线与
,所以抛物线与 轴的另一交点在对称轴的右侧,故函数
轴的另一交点在对称轴的右侧,故函数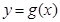 有一个零点在原点右侧,满足条件. (5分)
有一个零点在原点右侧,满足条件. (5分)综上可得,实数
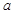 的取值范围是
的取值范围是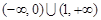 . (6分)
. (6分)(Ⅱ)假设函数
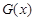 存在“中值相依切线”.
存在“中值相依切线”.设
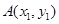 ,
,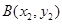 是曲线
是曲线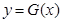 上的不同两点,且
上的不同两点,且 ,
,则
 ,
,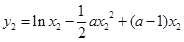 .
.

 (8分)
(8分)曲线在点
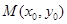 处的切线斜率
处的切线斜率

 , (9分)
, (9分)依题意得:

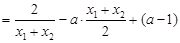 .
.化简可得:
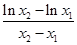
 , 即
, 即 =
=
 . (11分)
. (11分)设
 (
(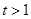 ),上式化为:
),上式化为: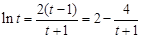 , 即
, 即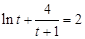 . (12分)
. (12分)令
 ,
,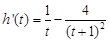
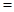
 .
.因为
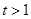 ,显然
,显然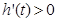 ,所以
,所以 在
在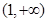 上递增,显然有
上递增,显然有 恒成立.
恒成立.所以在
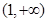 内不存在
内不存在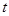 ,使得
,使得 成立.
成立. 综上所述,假设不成立.所以,函数
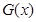 不存在“中值相依切线”. (14分)
不存在“中值相依切线”. (14分)
练习册系列答案
相关题目
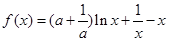 (
(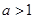 ).
).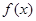 在区间
在区间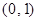 上的单调性;
上的单调性;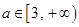 时,曲线
时,曲线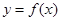 上总存在相异两点
上总存在相异两点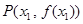 ,
,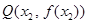 ,使得曲线
,使得曲线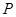 ,
,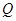 处的切线互相平行,求证:
处的切线互相平行,求证: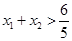 .
. 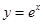 在点
在点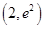 处的切线与坐标轴所围三角形的面积为 .
处的切线与坐标轴所围三角形的面积为 .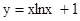
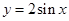 在点
在点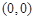 处的切线与直线
处的切线与直线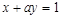 垂直,则实数
垂直,则实数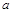 的值为( )
的值为( )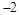
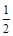
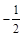
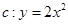 ,点
,点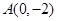 及点
及点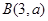 ,从点A观察B,要实现不被曲线C挡住,则实数
,从点A观察B,要实现不被曲线C挡住,则实数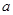 的取值范围是( )
的取值范围是( )
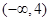


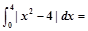 .
.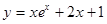 在点P(0,1)处的切线方程是__________。
在点P(0,1)处的切线方程是__________。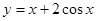 在区间
在区间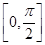 上的最大值是 .
上的最大值是 .