题目内容
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)在阅读量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人的成绩优秀,在阅量为
人的成绩优秀,在阅量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人成绩不优秀,请完成下面的
人成绩不优秀,请完成下面的![]() 列联表,并判断在“犯错误概率不超过
列联表,并判断在“犯错误概率不超过![]() ”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
阅读量为 | 阅读量为 | 合计 | |
成绩优秀的人数 | |||
成绩不优秀的人数 | |||
合计 |
(2)在抽出的同学中,1)求抽到被污染部分的同学人数;2)从阅读量在![]() 万到
万到![]() 万字及
万字及![]() 万到
万到![]() 万字的同学中选出
万字的同学中选出![]() 人写出阅读的心得体会.求这
人写出阅读的心得体会.求这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)列联表见解析,能在犯错误的概率不超过0.005的前提下认为“学生成绩优秀与阅读量有相关关系”.
(2)被污损部分的同学人数为10人; ![]() ..
..
【解析】试题分析:(1)第(1)问,先计算出阅读量在3万到5万的人数为50, 9万到11万的人数为125, 11万到13万的人数为75,再填表,最后求出随机变量![]() 的值,作出判断.(2)第(2)问,先利用频数公式计算出抽到被污染部分的同学人数,再利用古典概型计算出这
的值,作出判断.(2)第(2)问,先利用频数公式计算出抽到被污染部分的同学人数,再利用古典概型计算出这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
试题解析:
(I)阅读量在3万到5万的小矩形的面积为0.1,阅读量在9万到11万的小矩形的面积为0.25,阅读量在11万到13万的小矩形的面积为0.15.
![]() 阅读量在3万到5万的人数为50, 9万到11万的人数为125, 11万到13万的人数为75.
阅读量在3万到5万的人数为50, 9万到11万的人数为125, 11万到13万的人数为75.
则
阅读量为3万到5万人数 | 阅读量为11万到13万人数 | 合计 | |
成绩优秀的人数 | 20 | 50 | 70 |
成绩不优秀的人数 | 30 | 25 | 55 |
合计 | 50 | 75 | 125 |
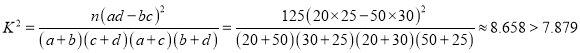 .
.
![]() 能在犯错误的概率不超过0.005的前提下认为“学生成绩优秀与阅读量有相关关系” .
能在犯错误的概率不超过0.005的前提下认为“学生成绩优秀与阅读量有相关关系” .
(II)
(1)由(I)知阅读量在5万到9万的小矩形的面积为1-(01+0.25+0.15)=0.5
则被污损部分的同学人数为10人,
(2)按分层抽样的方法,抽得阅读量在3万到5万的人数为2人,阅读量在11万字到13万字的为3人,
设阅读量在3万字到5万字的2个同学为![]() ,阅读量为11万字到13万字的3个同学为
,阅读量为11万字到13万字的3个同学为![]()
则从这8个同学中选出2个同学的情况有: ![]()
![]()
![]() ,共10种情况,
,共10种情况,
2人中恰有1人来自阅读量是11万到13万的有: ![]()
![]() ,共6种情况,
,共6种情况,
![]() ,
, ![]() 这2人中恰有1人来自阅读量是11万到13万的概率为
这2人中恰有1人来自阅读量是11万到13万的概率为![]() .
.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 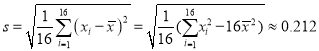 ,
, 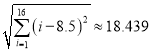 ,
, ![]() ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
(1)求![]()
![]() 的相关系数
的相关系数![]() ,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若
,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若![]() ,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在![]() 之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本![]()
![]() 的相关系数
的相关系数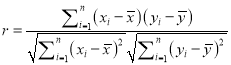 ,
, ![]() .
.