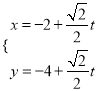题目内容
【题目】已知![]() ,若方程
,若方程![]() 有2个不同的实根,则实数
有2个不同的实根,则实数![]() 的取值范围是_____(结果用区间表示).
的取值范围是_____(结果用区间表示).
【答案】![]()
【解析】
由方程的解与函数图象的交点个数的关系可得![]() 有2个不同的实根等价于
有2个不同的实根等价于![]() 的图象与直线
的图象与直线![]() 的交点个数为2,由函数图象的性质及利用导数求切线方程可设过原点的直线与
的交点个数为2,由函数图象的性质及利用导数求切线方程可设过原点的直线与![]() 相切与点
相切与点![]() ,由
,由![]() ,则此切线方程为
,则此切线方程为![]() ,又此直线过原点
,又此直线过原点![]() ,则求得
,则求得![]() ,即切线方程为
,即切线方程为![]() 再结合图象可得实数
再结合图象可得实数![]() 的取值范围是
的取值范围是![]() ,得解.
,得解.
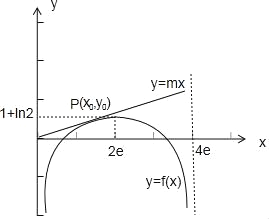
解:由![]() ,
,
可得:![]() 在
在![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
![]() 有2个不同的实根等价于
有2个不同的实根等价于![]() 的图象与直线
的图象与直线![]() 的交点个数为2,
的交点个数为2,
![]() 的图象与直线
的图象与直线![]() 的位置关系如图所示,
的位置关系如图所示,
设过原点的直线与![]() 相切与点
相切与点![]() ,
,
由![]() ,
,
则此切线方程为:![]() ,
,
又此直线过原点![]() ,
,
则求得![]() ,
,
即切线方程为:![]() ,
,
由图可知:当![]() 的图象与直线
的图象与直线![]() 的交点个数为2时,
的交点个数为2时,
实数![]() 的取值范围是
的取值范围是![]() ,
,
故答案为:![]() .
.

【题目】某地有一企业2007年建厂并开始投资生产,年份代号为7,2008年年份代号为8,依次类推.经连续统计9年的收入情况如下表(经数据分析可用线性回归模型拟合![]() 与
与![]() 的关系):
的关系):
年份代号( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
当年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)试预测2020年该企业的收入.
(参考公式: 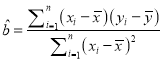
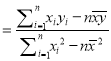 ,
, ![]() )
)
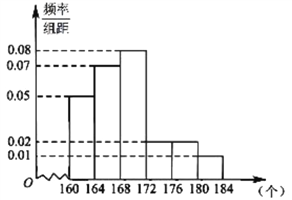
【题目】某校初一年级全年级共有![]() 名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为
名学生,为了拓展学生的知识面,在放寒假时要求学生在假期期间进行广泛的阅读,开学后老师对全年级学生的阅读量进行了问卷调查,得到了如图所示的频率分布直方图(部分已被损毁),统计人员记得根据频率直方图计算出学生的平均阅读量为![]() 万字.根据阅读量分组按分层抽样的方法从全年级
万字.根据阅读量分组按分层抽样的方法从全年级![]() 人中抽出
人中抽出![]() 人来作进一步调查.
人来作进一步调查.

(1)在阅读量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人的成绩优秀,在阅量为
人的成绩优秀,在阅量为![]() 万到
万到![]() 万字的同学中有
万字的同学中有![]() 人成绩不优秀,请完成下面的
人成绩不优秀,请完成下面的![]() 列联表,并判断在“犯错误概率不超过
列联表,并判断在“犯错误概率不超过![]() ”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
”的前提下,能否认为“学生成绩优秀与阅读量有相关关系”;
阅读量为 | 阅读量为 | 合计 | |
成绩优秀的人数 | |||
成绩不优秀的人数 | |||
合计 |
(2)在抽出的同学中,1)求抽到被污染部分的同学人数;2)从阅读量在![]() 万到
万到![]() 万字及
万字及![]() 万到
万到![]() 万字的同学中选出
万字的同学中选出![]() 人写出阅读的心得体会.求这
人写出阅读的心得体会.求这![]() 人中恰有
人中恰有![]() 人来自阅读量是
人来自阅读量是![]() 万到
万到![]() 万的概率.
万的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|