Question

9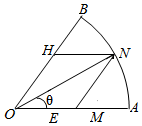．某房地产开发商为吸引更多的消费者购房，决定在一块闲置的扇形空地中修建一个花园，如图，已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$，半径为R，现欲修建的花园为平行四边形OMNH，其中M，H分别在OA，OB上，N在AB上，设∠MON=θ，平行四边形OMNH的面积为S．
1）将S表示为关于θ的函数；
（2）求S的最大值及相应的θ值．

Answer 1

分析 （1）分别过N，H作ND⊥OA于D，HE⊥OA于E，则HEDN为矩形，求出边长，即可求S关于θ的函数关系式；
（2）利用二倍角公式、两角和的正弦函数化简函数的表达式为一个角的一个三角函数的形式，通过θ的范围求出S的最大值及相应的θ角

解答 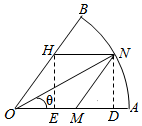解：（1）分别过N、H作ND⊥OA于D，HE⊥OA于E，HEDN为矩矩形（2分）
由扇形半径为R，ND=sinθON=Rsinθ，OD=Rcosθ，
在Rt△OEH中，∠AOB=$\frac{π}{4}$，OE=HE=ND，OM=OD-OE=Rcosθ-Rsinθ=$\sqrt{2}$Rcos（$θ+\frac{π}{4}$），
S=OM•ND=（Rcosθ-Rsinθ）Rsinθ=R²sinθcosθ-R²sin²θ=$\frac{1}{2}$R²sin2θ-R²×$\frac{1-cos2θ}{2}$=$\frac{{R}^{2}}{2}$（sin2θ+cos2θ）-$\frac{{R}^{2}}{2}$=$\frac{\sqrt{2}{R}^{2}}{2}$sin（2$θ+\frac{π}{4}$）-$\frac{{R}^{2}}{2}$；
（2）因为$θ∈（0，\frac{π}{4}）$，所以$2θ+\frac{π}{4}$∈（$\frac{π}{4}，\frac{3π}{4}$），所以sin（2$θ+\frac{π}{4}$）∈（$\frac{\sqrt{2}}{2}$，1]，所以S=$\frac{\sqrt{2}{R}^{2}}{2}$sin（2$θ+\frac{π}{4}$）-$\frac{{R}^{2}}{2}$∈（0，$\frac{\sqrt{2}-1}{2}{R}^{2}$]．
所以当$θ=\frac{π}{8}$时，S的最大值为$\frac{\sqrt{2}-1}{2}{R}^{2}$．

点评 本题是中档题，考查三角函数在解决实际问题中的应用，三角函数的化简求值，考查计算能力，转化思想的应用．