题目内容
11.设平面向量$\overrightarrow a$=(cosx,sinx),$\overrightarrow b$=$(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,函数f(x)=$\overrightarrow a•\overrightarrow b+1$.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)的单调递增区间.
分析 (Ⅰ)由平面向量数量积的运算,化简函数解析式可得f(x)=$sin(x+\frac{π}{3})+1$,由周期公式即可得解.
(Ⅱ)由$-\frac{π}{2}+2kπ≤x+\frac{π}{3}≤\frac{π}{2}+2kπ$即可解得f(x)的单调递增区间.
解答 解:(Ⅰ)$f(x)=(cosx,sinx)•(\frac{{\sqrt{3}}}{2},\frac{1}{2})+1$
=$\frac{1}{2}sinx+\frac{{\sqrt{3}}}{2}cosx+1$…2分
=$sin(x+\frac{π}{3})+1$…4分
所以,f(x)的最小正周期为2π.…6分
(Ⅱ)由$-\frac{π}{2}+2kπ≤x+\frac{π}{3}≤\frac{π}{2}+2kπ$…8分
得$-\frac{5π}{6}+2kπ≤x≤\frac{π}{6}+2kπ$…10分
所以,f(x)的单调递增区间为$[-\frac{5π}{6}+2kπ,\frac{π}{6}+2kπ](k∈Z)$.…12分.
点评 本题主要考查平面向量数量积的运算,三角函数的周期性及其求法,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1.复数$\frac{2i}{1-i}$的虚部是( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
19.“指数函数y=ax(a>1)是增函数,y=xα(α>1)是指数函数,所以y=xα(α>1)是增函数”,在以上演绎推理中,下列说法正确的是( )
| A. | 推理完全正确 | B. | 大前提不正确 | C. | 小前提不正确 | D. | 推理形式不正确 |
6.下列说法正确的是( )
| A. | log0.56>log0.54 | B. | 0.60.5>log0.60.5 | ||
| C. | 2.50<${(\frac{1}{2})^{2.5}}$ | D. | 90.9>270.48 |
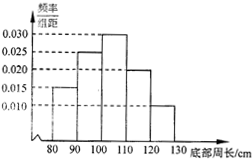 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.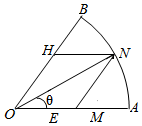 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.