题目内容
1.关于x的不等式$\frac{x}{{x}^{2}+16}$≤a≤$\frac{{x}^{2}+2}{x}$,对任意x∈(0,3]均成立,则实数a的取值范围为$\frac{3}{25}$≤a≤$\frac{11}{3}$.分析 构造函数,确定其单调性,求出函数的最值,即可确定实数a的取值范围.
解答 解:由题意,f(x)=$\frac{1}{x+\frac{16}{x}}$,而x+$\frac{16}{x}$在(0,3]上单调递减,∴f(x)max=$\frac{1}{3+\frac{16}{3}}$=$\frac{3}{25}$;
g(x)=$\frac{{x}^{2}+2}{x}$=x+$\frac{2}{x}$在(0,3]上单调递减,∴g(x)min=3+$\frac{2}{3}$=$\frac{11}{3}$,
∵关于x的不等式$\frac{x}{{x}^{2}+16}$≤a≤$\frac{{x}^{2}+2}{x}$,对任意x∈(0,3]均成立,
∴实数a的取值范围为$\frac{3}{25}$≤a≤$\frac{11}{3}$,
故答案为:$\frac{3}{25}$≤a≤$\frac{11}{3}$.
点评 本题考查恒成立问题,考查函数的最值,考查学生分析解决问题的能力,正确求最值是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.y=sin(ωx+$\frac{π}{6}$)(ω>0)在区间[-$\frac{3π}{4}$,$\frac{π}{2}$]上不单调,则ω的取值范围( )
| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,+∞) | C. | (0,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
10.在△ABC中,若asinA=bsinB,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
11.设函数f(x)的定义域为D,若函数f(x)满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域是[$\frac{a}{2}$,$\frac{b}{2}$],则称f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则实数t的取值范围是( )
| A. | (0,$\frac{1}{4}$) | B. | (-∞,$\frac{1}{4}$) | C. | (0,$\frac{1}{4}$] | D. | (-∞,$\frac{1}{4}$] |
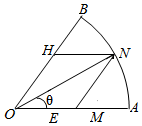 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.