题目内容
18.在正项等比数列{an}中a3+a4=$\frac{3}{8}$,a6=1,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为12.分析 设正项等比数列{an}首项为a1,公比为q,由题意可得关于这两个量的方程组,解之可得数列的通项公式和a1+a2+…+an及a1a2…an的表达式,化简可得关于n的不等式,解之可得n的范围,取上限的整数部分即可得答案.
解答 解:∵在正项等比数列{an}中a3+a4=$\frac{3}{8}$,a6=1,
∴a1q2(1+q)=$\frac{3}{8}$①,
a1q5=1②,q为数列的公比,
联立①②,解得a1=$\frac{1}{32}$,q=2,
∴Tn=a1+a2+…+an=$\frac{\frac{1}{32}(1-{2}^{n})}{1-2}$=$\frac{1}{32}$(2n-1),
Sn=a1a2…an=$(\frac{1}{32})^{n}$•21+2+…+n-1=${2}^{\frac{1}{2}{n}^{2}-\frac{11}{2}n}$.
由题意可得Tn>Sn,即$\frac{1}{32}$(2n-1)>${2}^{\frac{1}{2}{n}^{2}-\frac{11}{2}n}$,
化简得:2n-1>${2}^{\frac{1}{2}{n}^{2}-\frac{11}{2}n+5}$,即2n-${2}^{\frac{1}{2}{n}^{2}-\frac{11}{2}n+5}$>1,
因此只须n>$\frac{1}{2}{n}^{2}-\frac{11}{2}n+5$,即n2-13n+10<0
解得 $\frac{13-\sqrt{129}}{2}$<n<$\frac{13+\sqrt{129}}{2}$,
由于n为正整数,因此n最大为$\frac{13+\sqrt{129}}{2}$的整数部分,也就是12.
故答案为:12.
点评 本题考查等比数列的求和公式和一元二次不等式的解法,属中档题.

| A. | (0,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,+∞) | C. | (0,$\frac{2}{3}$] | D. | [$\frac{2}{3}$,+∞) |
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
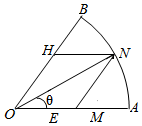 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.