题目内容
20.已知数列{an},a1=3,${a_{n+1}}=\frac{{3{a_n}-4}}{{{a_n}-1}}$,(n∈N*).(Ⅰ)求a2,a3,a4的值;
(Ⅱ)猜想an的通项公式,并用数学归纳法加以证明.
分析 ( I)由a1=3,且${a_{n+1}}=\frac{{3{a_n}-4}}{{{a_n}-1}}$,分别令n=1,2,3,即可得出;
( II)由(1)猜想${a_n}=\frac{2n+1}{n}$,利用数学归纳法进行证明即可.
解答 解:( I)∵a1=3,且${a_{n+1}}=\frac{{3{a_n}-4}}{{{a_n}-1}}$,
∴${a_2}=\frac{3×3-4}{3-1}=\frac{5}{2}$,${a_3}=\frac{{3×\frac{5}{2}-4}}{{\frac{5}{2}-1}}=\frac{7}{3}$,${a_4}=\frac{{3×\frac{7}{3}-4}}{{\frac{7}{3}-1}}=\frac{9}{4}$;
( II)由(1)猜想${a_n}=\frac{2n+1}{n}$,下面用数学归纳法进行证明.
①当n=1时,${a_1}=\frac{2×1+1}{1}=3$,满足要求,猜想成立;
②假设n=k(k≥1且k∈N*)时,猜想成立,即${a_k}=\frac{2k+1}{k}$,
那么当n=k+1时,${a_{k+1}}=\frac{{3{a_k}-4}}{{{a_k}-1}}=\frac{{3×\frac{2k+1}{k}-4}}{{\frac{2k+1}{k}-1}}=\frac{2k+3}{k+1}=\frac{{2({k+1})+1}}{k+1}$,
这就表明当n=k+1时,猜想成立.
根据(1),(2)可以断定,对所有的正整数该猜想成立,即${a_n}=\frac{2n+1}{n}$.
点评 本题考查了数学归纳法的应用、观察分析猜想归纳能力,考查了计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{1}{2}x(x<0)}\\{ln(x+1)(x≥0)}\end{array}\right.$,若函数y=f(x)-kx有3个零点,则实数k的取值范围为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},1)$ | C. | (1,+∞) | D. | $(\frac{1}{4},1)$ |
10.在△ABC中,若asinA=bsinB,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 等边三角形 |
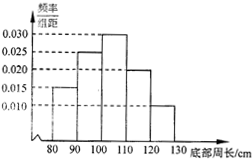 为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.
为了了解一片经济林的生长情况,随机抽 测了其中80株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的80株树木中,有32株树木的底部周长小于100cm.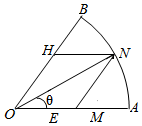 某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.
某房地产开发商为吸引更多的消费者购房,决定在一块闲置的扇形空地中修建一个花园,如图,已知扇形AOB的圆心角∠AOB=$\frac{π}{4}$,半径为R,现欲修建的花园为平行四边形OMNH,其中M,H分别在OA,OB上,N在AB上,设∠MON=θ,平行四边形OMNH的面积为S.